Geometrische Bedeutung der Kleinheit der Differenzierung
Es ist sinnvoll, zu prüfen, welche geometrische Bedeutung dem Differentialkoeffizienten gegeben werden kann.
Zunächst kann jede Funktion von x, wie zum Beispiel x2 oder $\sqrt{x}$ oder $ax+b$, als Kurve gezeichnet werden; und heutzutage kennt jeder Schüler das Verfahren des Kurvenzeichnens.
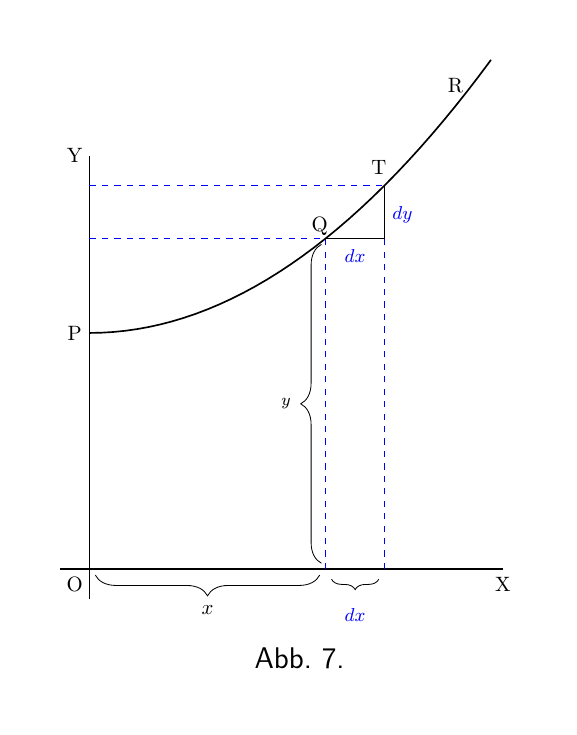
Lassen Sie PQR, in Abbildung 7, ein Teil einer Kurve sein, die in Bezug auf die Koordinatenachsen OX und OY aufgetragen ist. Betrachten Sie einen beliebigen Punkt Q auf dieser Kurve, wobei die Abszisse des Punktes x und seine Ordinate y ist. Beobachten Sie nun, wie sich y ändert, wenn x variiert wird. Wenn man x um ein kleines Inkrement dx nach rechts ansteigen lässt, wird man beobachten, dass auch y (in dieser speziellen Kurve) um ein kleines Inkrement dy ansteigt (weil diese spezielle Kurve zufällig eine steigende Kurve ist). Dann ist das Verhältnis von dy zu dx ein Maß für den Grad, in dem die Kurve zwischen den beiden Punkten Q und T ansteigt. Tatsächlich kann man auf der Abbildung sehen, dass die Kurve zwischen Q und T viele verschiedene Steigungen hat, so dass man nicht sehr gut von der Steigung der Kurve zwischen Q und T sprechen kann. Wenn aber Q und T so nahe beieinander liegen, dass der kleine Teil QT der Kurve praktisch gerade ist, dann kann man sagen, dass das Verhältnis $\dfrac{dy}{dx}$ die Steigung der Kurve entlang QT ist. Die zwischen beiden Punkten (Punkt Q und Punkt T) erzeugte Gerade QT berührt die Kurve nur entlang des Teils QT, und wenn dieser Teil unendlich klein ist, dann berührt die Gerade die Kurve praktisch nur in einem Punkt und ist daher eine Tangente an die Kurve.
Diese Tangente an der Kurve hat offensichtlich die gleiche Steigung wie QT, so dass $\dfrac{dy}{dx}$ die Steigung der Tangente an der Kurve in dem Punkt Q ist, für den der Wert von $\dfrac{dy}{dx}$ gefunden wird.
Wir haben gesehen, dass der kurze Ausdruck die Steigung einer Kurve keine genaue Bedeutung hat, weil eine Kurve so viele Steigungen hat - tatsächlich hat jeder kleine Teil einer Kurve eine andere Steigung. Die Steigung einer Kurve an einem Punkt ist jedoch eine genau definierte Sache; sie ist die Steigung eines sehr kleinen Teils der Kurve, der sich genau an diesem Punkt befindet; und wir haben gesehen, dass dies dasselbe ist wie die Steigung der Tangente an der Kurve an diesem Punkt.
Beachten Sie, dass dx ein kurzer Schritt nach rechts ist, und dy der entsprechende kurzer Schritt nach oben. Diese Schritte müssen als so kurz wie möglich betrachtet werden - tatsächlich unendlich kurz -, obwohl wir sie in Diagrammen durch nicht unendlich kleine Teile darstellen müssen, da man sie sonst nicht sehen könnte.
Wir werden im Folgenden viel Gebrauch von dem Umstand machen, dass $\dfrac{dy}{dx}$ die Steigung der Kurve an jedem Punkt darstellt.
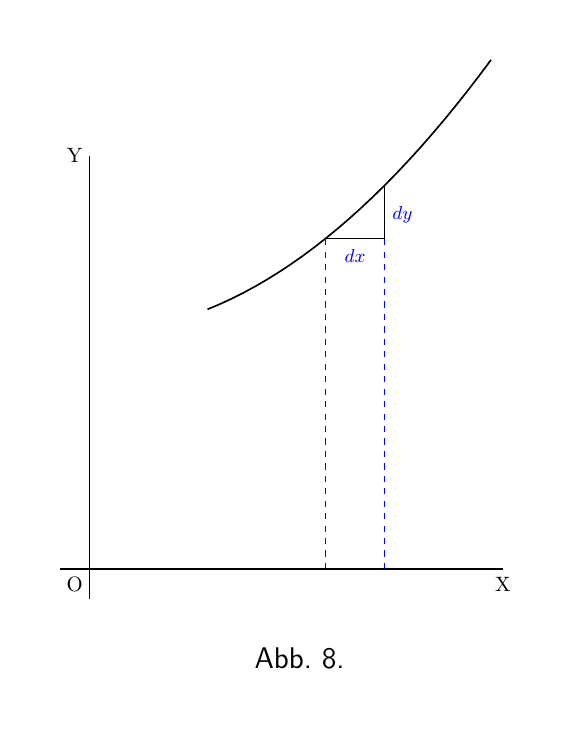
Wenn eine Kurve, an einem bestimmten Punkt, eine Steigung von 45° besitzt, wie in Abbildung 8, dann sind dy und dx gleich, und der Wert von $\dfrac{dy}{dx}$ ist $\dfrac{dy}{dx} = 1$.
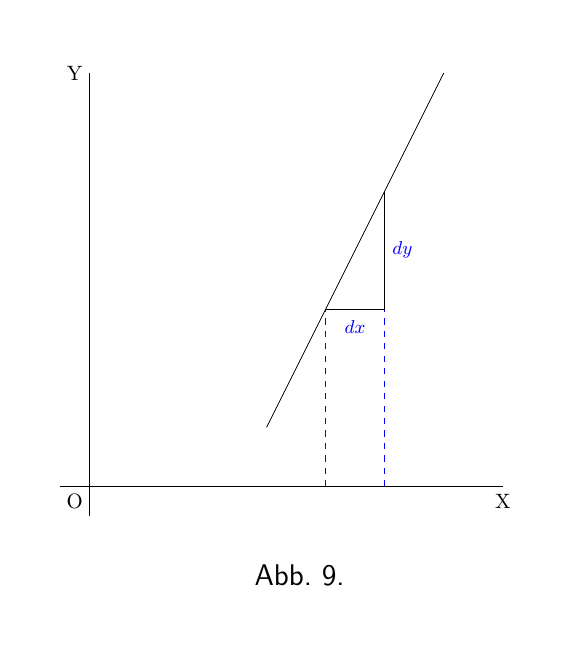
Wenn die Steigung der Kurve steiler als 45 ° (Abbildung 9) ist, das ist $\dfrac{dy}{dx}$ größer als 1.
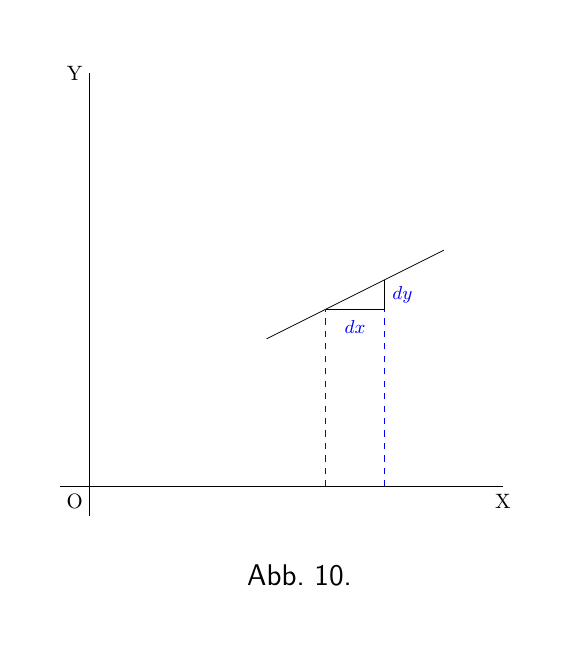
Wenn die Steigung der Kurve flacher als 45 ° verläuft, wie in Abbildung 10, dann ist $\dfrac{dy}{dx}$ kleiner wie 1.
Bei einer horizontalen Linie beziehungsweise bei einem horizontalen Abschnitt einer Kurve ist $dy=0$, und damit $\dfrac{dy}{dx}=0$.
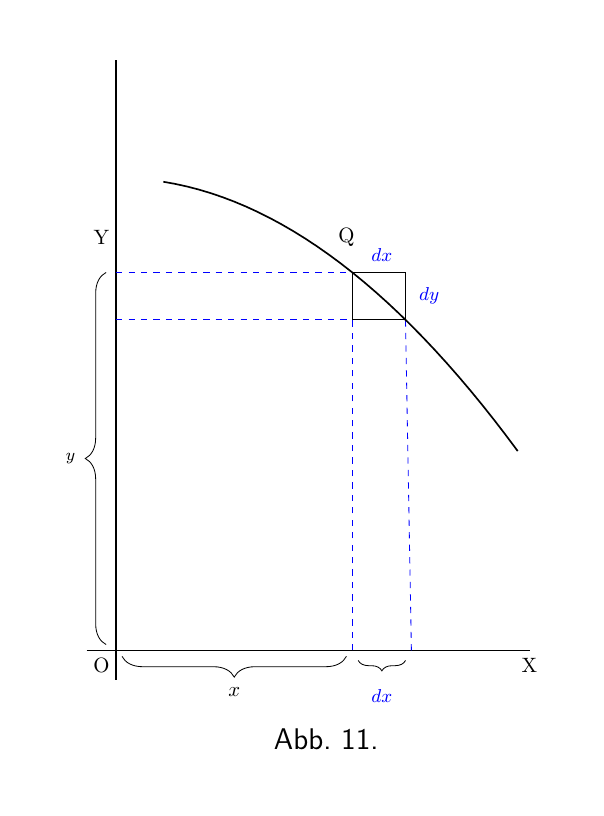
Wenn die Kurve nach unten verläuft, beziehungsweise abwärts gerichtet ist, wie in Abbildung 11, dann ist dy ein Schritt nach unten und es muss daher mit einem negativen Wert gerechnet werden; aus diesem Grund hat $\dfrac{dy}{dx}$ ein negatives Vorzeichen.
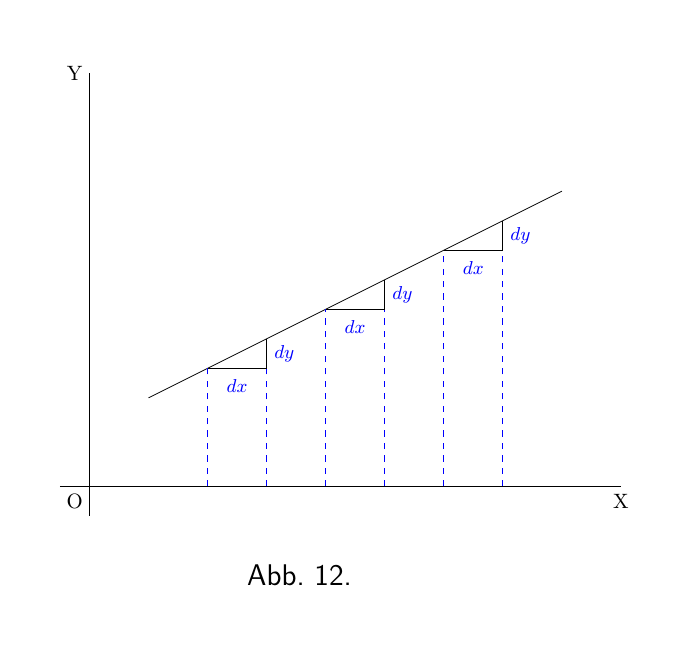
Wenn es sich bei der Kurve um eine gerade Linie handelt, wie in Abbildung 12, dann ist der Wert von $\dfrac{dy}{dx}$ in allen Punkten (auf dieser Linie) gleich. Mit anderen Worten die Steigung ist konstant.
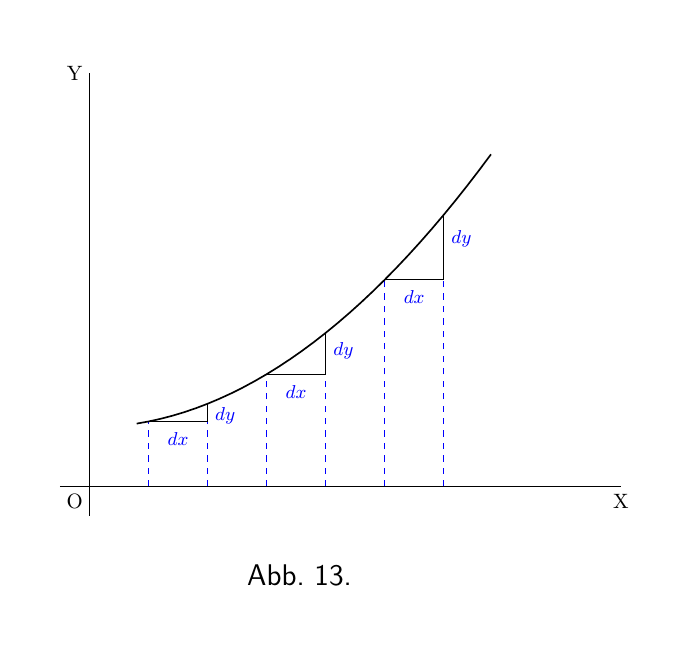
Bei einer Kurve, die mehr nach oben wie nach rechts geht, wird der Wert von $\dfrac{dy}{dx}$ mit zunehmender Steilheit größer und größer, wie in Abbildung 13.
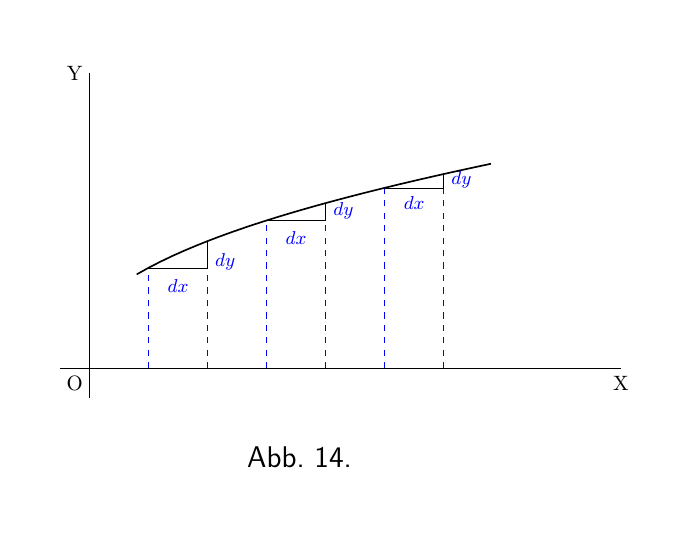
Wenn die Kurve immer mehr abflacht, wird der Wert von $\dfrac{dy}{dx}$ immer kleiner, wenn der flachere Teil erreicht wird, wie in Abbildung 14.
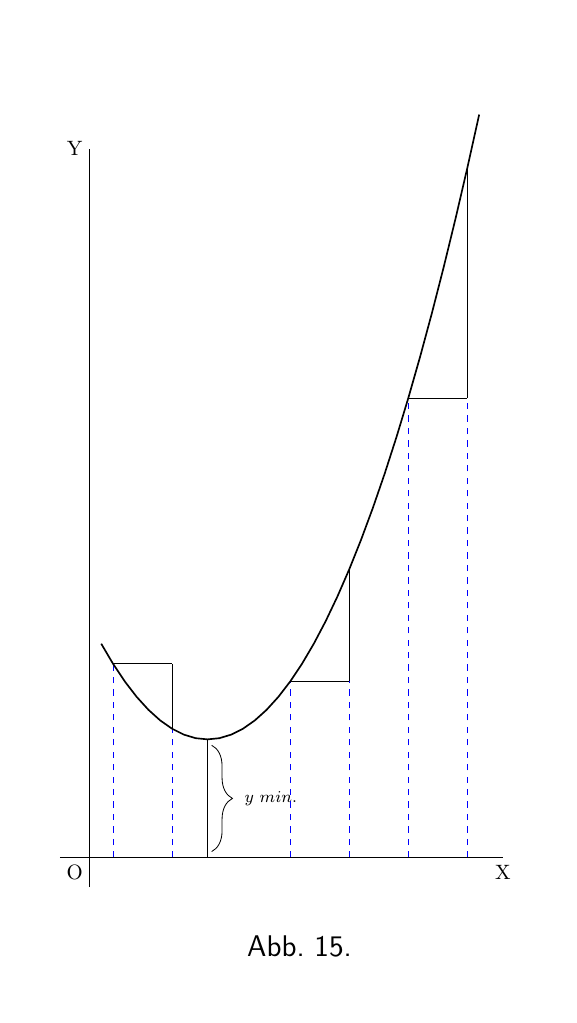
Wenn eine Kurve zuerst absteigt und dann wieder ansteigt, wie in Abbildung 15, und dabei eine Konkavität nach oben aufweist, dann wird $\dfrac{dy}{dx}$ zuerst eindeutig negativ sein, mit abnehmenden Werten, während die Kurve abflacht, und an dem Punkt, an dem der Tiefpunkt der Kurve erreicht wird, Null sein; und von diesem Punkt an wird $\dfrac{dy}{dx}$ positive Werte haben, die immer weiter ansteigen. In einem solchen Fall sagt man, dass y ein Minimum durchläuft. Der Minimalwert von y ist nicht notwendigerweise der kleinste Wert von y, es ist derjenige Wert von y, der dem Boden des Tales entspricht; zum Beispiel in Abbildung 28 ist der Wert von y, der dem Boden des Tales entspricht, 1, während y an anderen Stellen Werte annehmen kann, die kleiner als 1 sind. Die Eigenschaft eines Minimums ist, dass y auf beiden Seiten davon zunehmen muss.
Hinweis An dem Wert von x bei dem y ein Minimum durchläuft, ist der Wert von $\dfrac{dy}{dx} = 0$.
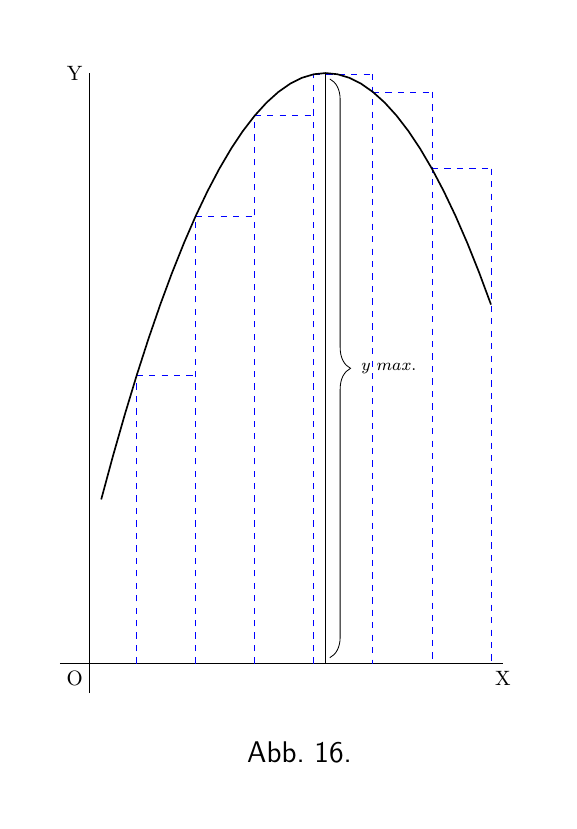
Wenn eine Kurve zuerst auf- und dann abfällt, sind die Werte von $\dfrac{dy}{dx}$ zunächst positiv; dann null, wenn der Gipfel erreicht ist; dann negativ, wenn die Kurve nach unten abfällt, wie in Abbildung 16. In diesem Fall wird gesagt, dass y ein Maximum durchläuft / durchschreitet, aber der Wert von y in diesem Maximum, ist nicht unbedingt der größte Wert von y. In Abbildung 28 beträgt der Wert vom y im Maximum $2\frac{1}{3}$, aber dies ist keineswegs der größte Wert, den y an einem anderen Punkt der Kurve haben kann.
Hinweis An dem Wert von x bei dem y ein Maximum durchläuft, ist der Wert von $\dfrac{dy}{dx} = 0$.
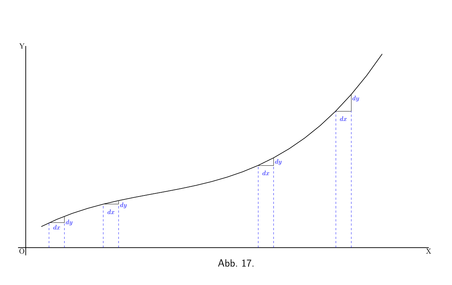
Wenn eine Kurve die besondere Form von Abbildung 17 hat, sind die Werte von $\dfrac{dy}{dx}$ immer positiv; es wird jedoch einen bestimmten Ort geben, an dem die Steigung am wenigsten steil beziehungsweise am geringsten ist, an dem der Wert von $ \dfrac{dy}{dx} $ minimal sein wird. Das heißt, kleiner als an jedem anderen Teil der Kurve.
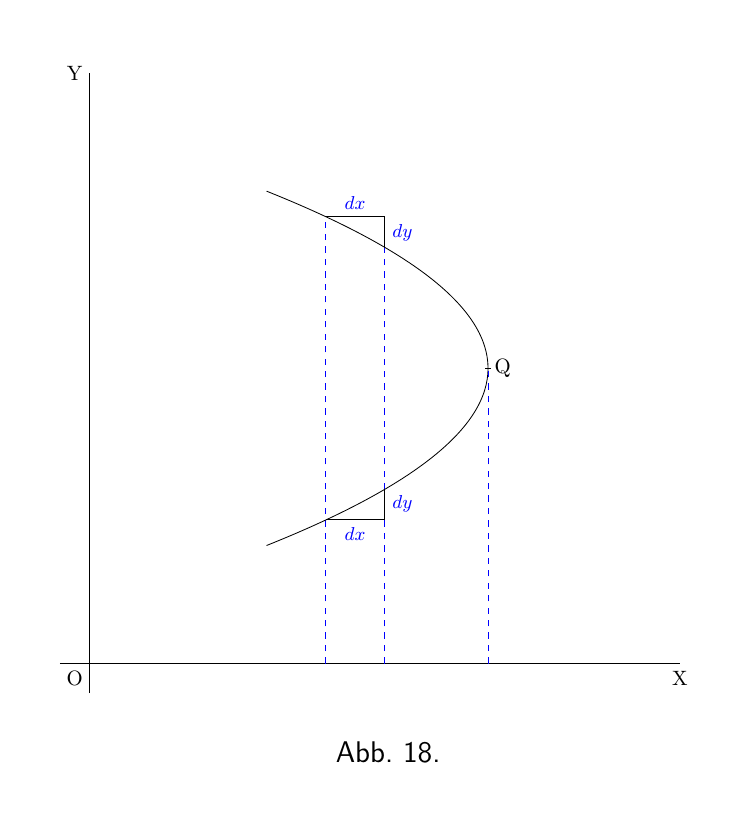
Wenn eine Kurve die Form von Abbildung 18 hat, ist der Wert von $\dfrac{dy}{dx}$ im oberen Teil negativ und im untere Teil positiv; während an der Beule der Kurve, wo die Steigung der Kurve senkrecht wird, ist der Wert von $\dfrac{dy}{dx}$ unendlich groß.
Da wir nun verstehen, dass $\dfrac{dy}{dx}$ die Steigung einer Kurve an jedem Punkt misst, wenden wir uns nun einigen der Gleichungen zu, deren Differenzierung wir bereits gelernt haben.
(1) Nehmen Sie dies als den einfachsten Fall:
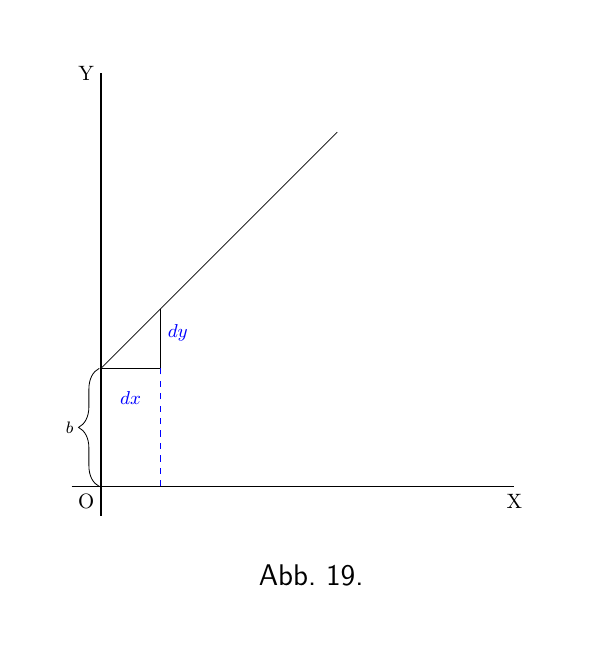
\[ y=x+b. \]
Die Funktion ist in Abbildung 19 dargestellt, wobei gleiche Skalen für x und y verwendet werden. Wenn wir $x = 0$ setzen, dann ist, die entsprechende Ordinate $y = b$; d.h. die Kurve schneidet die y-Achse auf der Höhe beziehungsweise beim Wert b. Von hier aus steigt die Kurve mit 45 ° an; für alle Werte, die rechts von x liegen, haben wir eine Zunahme der Höhe von y im gleichen Maß. Die Linie hat eine Steigung von 1, im Punkt $x = 1$.
Differenzieren Sie $y = x+b$ mit den Regeln die Sie bereits (hier und hier) gelernt haben, und wir erhalten $\dfrac{dy}{dx} = 1$.
Die Steigung der Linie ist so, dass wir für jeden kleinen Schritt dx nach rechts einen gleichen kleinen Schritt dy nach oben gehen. Und diese Steigung ist konstant - immer die gleiche Steigung.
(2) Betrachten Sie diesen Fall:
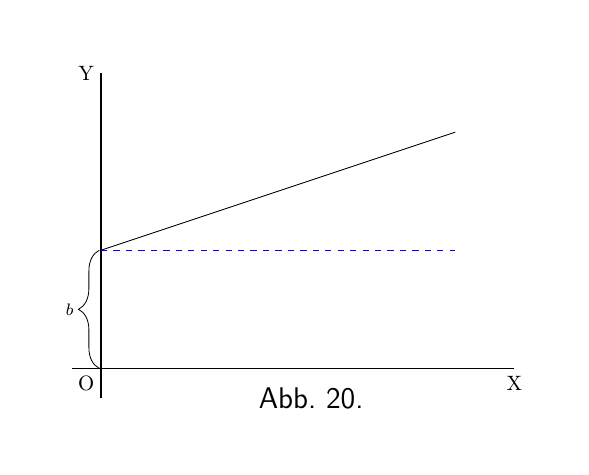
\[ y = ax+b. \]
Wir wissen, dass diese Kurve wie die vorhergehende bei einer Höhe von b auf der y-Achse beginnt. Aber bevor wir die Kurve zeichnen, wollen wir ihre Steigung durch Differenzieren ermitteln; was $\dfrac{dy}{dx} = a$ ergibt. Die Steigung wird konstant sein, in einem Winkel, dessen Tangens hier a genannt wird. Lassen Sie uns a einen numerischen Wert zuweisen, sagen wir $\frac{1}{3}$. Dann müssen wir ihm eine solche Steigung geben, dass er um 1 ansteigt, wenn wir 3 Schritte nach rechts gehen; anders ausgedrückt dx ist 3 mal so groß wie dy; wie in Abbildung 21 vergrößert dargestellt wird. Zeichnen Sie also eine Linie wie in Abbildung 20 mit dieser Steigung.
(3) Ein etwas schwierigerer Fall. Sei
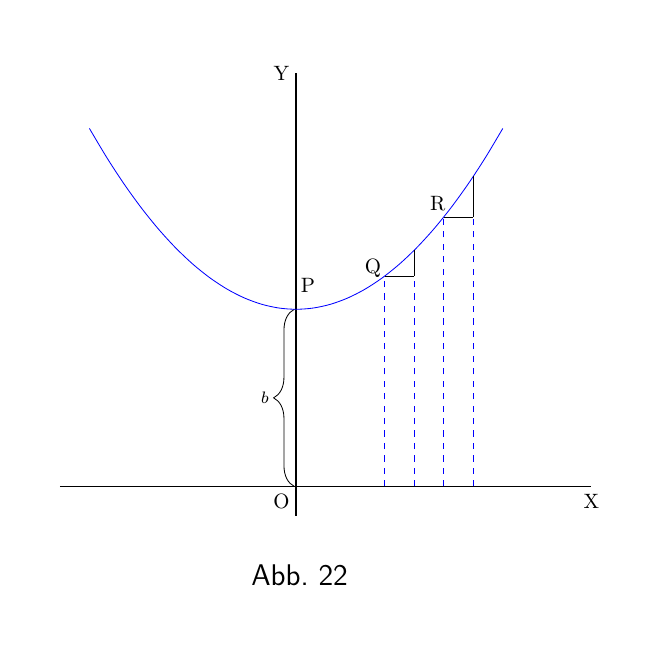
\begin{align*} y= ax^2 + b. \end{align*}
Wieder beginnt die Kurve auf der y-Achse in einer Höhe b über dem Ursprung.
Jetzt differenzieren. [Wenn Sie das Ergebnis vergessen haben, gehen Sie hier zurück; oder besser: nicht umkehren, sondern die Differenzierung selbst berechnen.]
\[ \frac{dy}{dx} = 2ax. \]
Dies zeigt, dass die Steilheit nicht konstant ist: Sie nimmt mit steigendem x zu. Am Startpunkt P, wo $x = 0$, hat die Kurve (Abbildung 22) keine Steilheit, d.h. sie ist eben. Links vom Ursprung, wo x negative Werte hat, wird $\dfrac{dy}{dx}$ ebenfalls negative Werte haben oder von links nach rechts absteigen, wie in der Abbildung.
Lassen Sie uns dies veranschaulichen, indem wir einen bestimmten Fall herausarbeiten. Wir nehmen die Gleichung
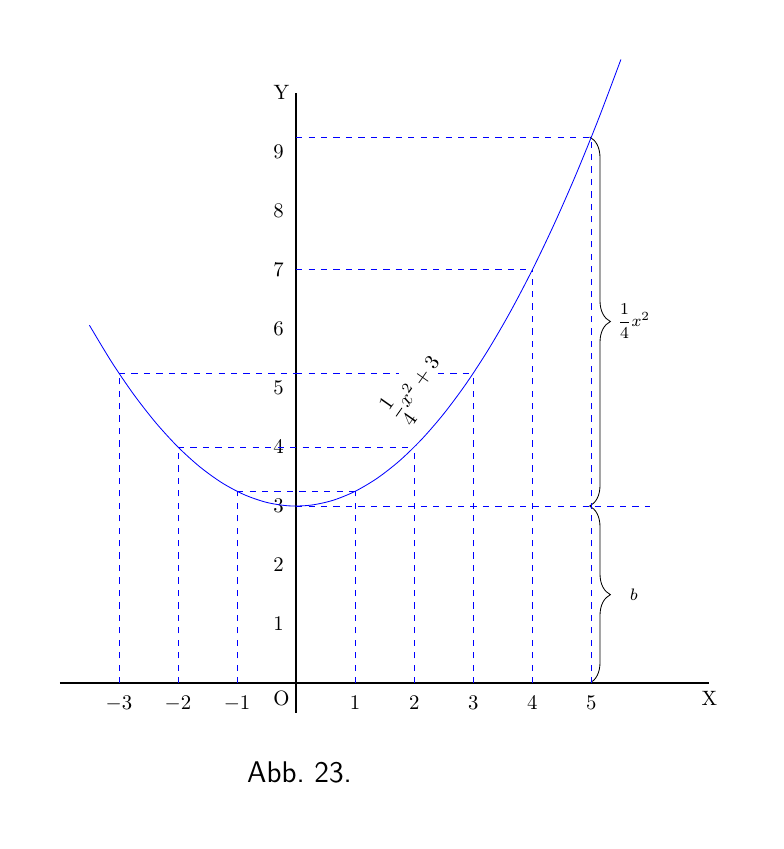
\[ y = \tfrac{1}{4}x^2 + 3, \]
und differenzieren diese, dann erhalten wir
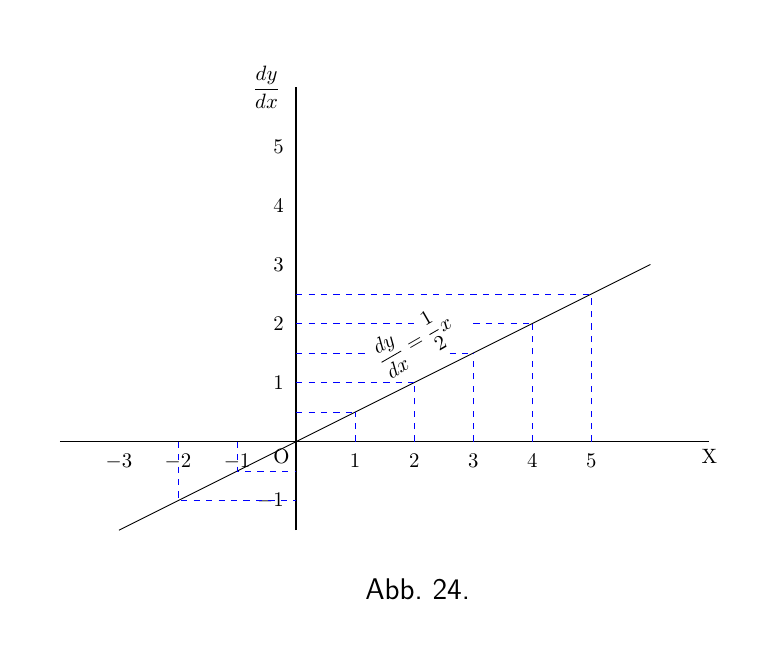
\[ \dfrac{dy}{dx} = \tfrac{1}{2}x. \]
Erstellen Sie nun eine Wertetabelle mit einige aufeinanderfolgende Werte zu, sagen wir von 0 bis 5 für x; und berechne die entsprechenden Werte von y mit der ersten Gleichung; und die Werte von $\dfrac{dy}{dx}$ mit der zweiten Gleichung. Als Ergebnisse haben wir:
| x | 0 | 1 | 2 | 3 | 4 | 5 |
| y | 3 | $3\frac{1}{4}$ | 4 | $5\frac{1}{4}$ | 7 | $9\frac{1}{4}$ |
| d | 0 | $\frac{1}{2}$ | 1 | $1\frac{1}{2}$ | 2 | $2\frac{1}{2}$ |
Dann stellen Sie die Werte in zwei Kurven dar, indem Sie Abbildung 23 die Werte von y gegen die von x und in Abbildung 24 die von $\dfrac{dy}{dx}$ gegenüber denen von x auftragen. Für jeden zugewiesenen Wert von x ist die Höhe der Ordinate in der zweiten Kurve proportional zur Steigung der ersten Kurve.
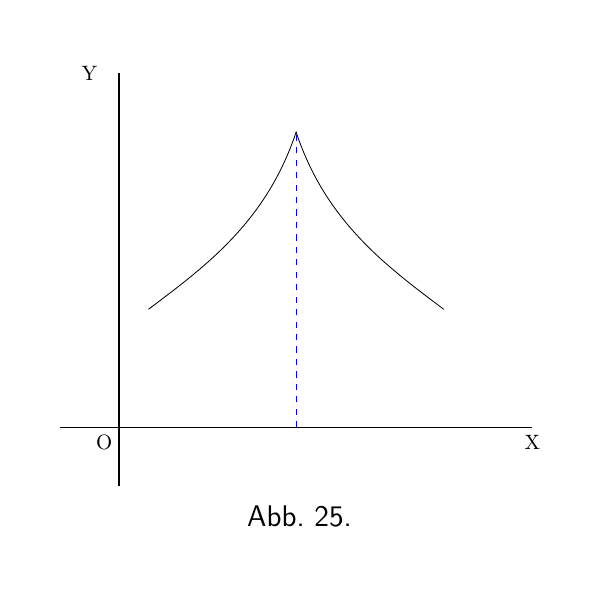
Wenn eine Kurve einen plötzlichen Scheitelpunkt erreicht, wie in Abbildung 25, ändert sich die Steigung an diesem Punkt plötzlich von einer Steigung nach oben zu einer Steigung nach unten. In diesem Fall wird $\dfrac{dy}{dx}$ von einem positiven zu einem negativen Wert wechseln.
Die folgenden Beispiele zeigen weitere Anwendungen der soeben erläuterten Prinzipien.
(4) Ermitteln Sie die Steigung der Tangente an der Kurve
\[ y = \frac{1}{2x} + 3, \]
an der Stelle, an der $x = -1$ ist. Bestimmen Sie den Winkel, den diese Tangente mit der Kurve $y = 2x^2 + 2$ bildet.
Die Steigung der Tangente ist die Steigung der Kurve an dem Punkt, an dem sie sich berühren (siehe hier); das heißt, die Steigung der Tangente entspricht $\dfrac{dy}{dx}$ der Kurve für diesen Punkt. Hier ist $\dfrac{dy}{dx} = -\dfrac{1}{2x^2}$ und für $x = -1$ ist $\dfrac{dy}{dx} = -\dfrac{1}{2 }$, das ist die Steigung der Tangente und der Kurve an dem (Berühr-)Punkt. Die Tangente, ist eine Gerade, die die Gleichung $y = ax + b$ hat und ihre Steigung ist $\dfrac{dy}{dx} = a$, also ist $a = -\dfrac{1}{2}$ . Wenn $x= -1$, $y = \dfrac{1}{2(-1)} + 3 = 2\frac{1}{2}$; und wenn die Tangente an diesem Punkt vorbeiläuft, müssen die Koordinaten des Punktes die Tangentengleichung erfüllen, nämlich
\[ y = -\dfrac{1}{2} x + b, \]
sodass $2\frac{1}{2} = -\dfrac{1}{2} \times (-1) + b$ und $b = 2$ gilt; die Tangentengleichung ist daher $y = -\dfrac{1}{2} x + 2$.
Wenn sich nun zwei Kurven treffen, wobei der Schnittpunkt ein für beide Kurven gemeinsamer Punkt ist, müssen die Koordinaten des gemeinsamen Punktes die Gleichung jeder der beiden Kurven erfüllen; das heißt, es muss eine Lösung des Systems simultaner Gleichungen sein, die durch Verknüpfung der Gleichungen der Kurven gebildet werden. Hier treffen die Kurven an Punkten aufeinander, die durch die Lösung von
\begin{aligned} y &= 2x^2 + 2, \\ y &= -\tfrac{1}{2} x + 2 \quad\text{bzw.}\quad 2x^2 + 2 = -\tfrac{1}{2} x + 2; \end{aligned}
gegeben sind, das ist,
\[ x(2x + \tfrac{1}{2}) = 0. \]
Diese Gleichung hat $x = 0$ und $x = -\tfrac{1}{4}$ als Lösung. Die Steigung der Kurve $y = 2x^2 + 2$ ist an jedem Punkt
\[ \dfrac{dy}{dx} = 4x. \]
An dem Punkt, an dem $x = 0$ ist, ist die Steigung null; die Kurve ist horizontal. Für den Punkt wo folgendes gilt:
\[ x = -\dfrac{1}{4},\quad \dfrac{dy}{dx} = -1; \]
Damit fällt die Kurve an diesem Punkt unter einem solchen Winkel $\theta$ mit der Horizontalen nach rechts ab, dass $\tan \theta = 1$ ist; also unter 45 ° zur Horizontalen.
Die Steigung der Geraden beträgt $-\tfrac{1}{2}$; das heißt, sie fällt nach rechts ab und bildet mit der Horizontalen einen Winkel φ mit $\tan\phi = \tfrac{1}{2}$; das heißt, ein Winkel von $26^{\circ} 34'$. Daraus folgt, dass die Kurve im ersten Punkt die Gerade unter einem Winkel von $26^{\circ} 34'$ schneidet, während sie diese im zweiten unter einem Winkel von $45^{\circ} - 26^{\circ } 34' = 18^{\circ} 26'$ schneidet.
(5) Es soll eine Gerade gezogen werden, durch einen Punkt dessen Koordinaten $x = 2$, $y = -1$ sind, als Tangente an die Kurve $y = x^2 - 5x + 6$. Finden Sie die Koordinaten des Berührungspunktes.
Die Steigung der Tangente muss mit $\dfrac{dy}{dx}$ der Kurve übereinstimmen; das heißt, $2x - 5$.
Die Geradengleichung ist $y = ax + b$, und da sie für die Werte $x = 2$, $y = -1$ erfüllt ist, dann ist $-1 = a \times 2 + b $; außerdem ist $\dfrac{dy}{dx} = a = 2x - 5$.
x und y des Berührungspunktes müssen auch sowohl die Tangentengleichung als auch die Kurvengleichung erfüllen.
Wie haben dann
\begin{align*} y &= x^2 - 5x + 6, \tag{i} \\ \end{align*} \begin{align*} y &= ax + b, \tag{ii} \\ \end{align*} \begin{align*} -1 &= 2a + b, \tag{iii} \\ \end{align*} \begin{align*} a &= 2x - 5, \tag{iv} \end{align*}
vier Gleichungen mit a, b, x, y.
Gleichung (i) und (ii) ergeben $x^2 - 5x + 6 = ax+b$.
Ersetzen von a und b durch ihre Werte und wir erhalten,
\[ x^2 - 5x + 6 = (2x - 5)x - 1 - 2(2x - 5), \]
was zu $x^2 - 4x + 3 = 0$ vereinfacht werden kann, die Lösungen sind: $x = 3$ und $x = 1$. Ersetzen in (i), wir bekommen $y = 0$ beziehungsweise $y = 2$; die zwei Berührungspunkte sind dann $x = 1$, $y = 2$, und $x = 3$, $y = 0$.
Hinweis.- Bei allen Übungen, die sich mit Kurven befassen, ist es für die Schüler äußerst lehrreich, die Folgerung durch tatsächliches Zeichnen der Kurven zu überprüfen.
Übungen VIII
(1) Zeichnen Sie die Kurve mit der Gleichung $y = \tfrac{3}{4} x^2 - 5$, verwenden Sie dabei eine Millimeter Skalierung. Messen Sie für verschiedene Werte von x den Winkel der Steigung.
Bestimmen Sie durch Differenzieren der Gleichung den Ausdruck für die Steigung; und überprüfen Sie anhand des Tangens, ob diese mit dem gemessenen Winkel übereinstimmt.
(2) Bestimmen Sie die Steigung der Kurve
\[ y = 0,12x^3 - 2, \]
wenn der Wert der Abzisse $x = 2$ beträgt.
(3) Wenn $y = (x - a)(x - b)$ ist, zeigen Sie das am Punkt der Kurve wo $\dfrac{dy}{dx} = 0$ beträgt, x den Wert $\tfrac{1}{2} (a + b)$ hat.
(4) Bestimmen Sie $\dfrac{dy}{dx}$ von der Gleichung $y = x^3 + 3x$; und berechnen Sie die numerischen Werte von $\dfrac{dy}{dx}$ für die Punkte, die mit $x = 0$, $x = \tfrac{1}{2}$, $x = 1$, $x = 2$ korrespondieren.
(5) Bestimmen Sie in der Kurve, die durch die Gleichung $x^2 + y^2 = 4$ beschrieben wird, und die Werte von x an den Punkten, an denen die Steigung ${} = 1$ ist.
(6) Bestimmen Sie die Steigung, deren Gleichung $\dfrac{x^2 }{3^2} + \dfrac{y^2}{2^2} = 1$, an einem beliebigen Punkt und geben Sie den numerischen Wert, der Steigung an der Stelle $x = 0$ und $x = 1$ an.
(7) Die Gleichung einer Tangente an die Kurve $y = 5 - 2x + 0,5x^3$, ist von der Form $y = mx + n$, wobei $m$ und n Konstanten sind, bestimmen Sie den Wert von $m$ und n wenn der Punkt, an dem die Tangente die Kurve berührt, $x=2$ als Abszisse hat.
(8) In welchem Winkel schneiden sich die beiden Kurven
\[ y = 3,5x^2 + 2 \quad \text{und} \quad y = x^2 - 5x + 9,5 \text{?} \]
(9) Die Tangenten an die Kurve $y = \pm \sqrt{25-x^2}$ werden an Punkten gezeichnet, für die $x = 3$ und $x = 4$ ist. Bestimmen Sie die Koordinaten des Schnittpunktes der Tangenten und ihrer gegenseitigen Neigung.
(10) Eine gerade Linie $y = 2x - b$ berührt, eine Kurve $y = 3x^2 + 2$ an einem Punkt. Was für Koordinaten hat dieser Berührungspunkt, und wie ist der Wert von b?
Antworten
(2) $1,44$.
(4) $\dfrac{dy}{dx} = 3x^2 + 3$; und die numerischen Werte sind: 3, $3 \frac{3}{4}$, $6$, und $15$.
(5) $ \pm \sqrt{2}$.
(6) $ \dfrac{dy}{dx} = - \dfrac{4}{9} \dfrac{x}{y}$. Die Steigung ist null, bei $x = 0$; und ist $\mp \dfrac{1}{3 \sqrt{2}}$ wenn $x = 1$ ist.
(7) $m = 4$, $n = -3$.
(8) Schnittpunkt bei $x = 1$, $x = -3$. Winkel $153^{\circ}\;26'$, $2^{\circ}\;28'$.
(9) Schnittpunkt bei $x = 3.57$, $y = 3.50$. Winkel $16^{\circ}\;16'$.
(10) $x = \frac{1}{3}$, $y = 2 \frac{1}{3}$, $b = -\frac{5}{3}$.