Nächste Stufe. Was tun mit Konstanten

In unseren Gleichungen haben wir x als wachsend angesehen, und als Ergebnis der Veränderung von x haben wir auch gesehen, dass sich der Wert von y verändert und wächst. Bei x denken wir normalerweise an eine Menge, die wir variieren können; und, in Bezug auf die Variation von x können wir die Variation als eine Art Ursache und die daraus resultierende Variation von y als Effekt betrachten. Mit anderen Worten, wir betrachten den Wert von y als abhängig von dem Wert von x. Sowohl x als auch y sind Variablen, aber x ist diejenige, mit der wir arbeiten, und y ist die abhängige Variable. In allen vorhergehenden Kapiteln haben wir versucht, Regeln, die das Verhältnis der Variation zwischen der abhängigen Variable y und der unabhängigen Variable x beschreiben zu finden.

Unser nächster Schritt, besteht darin herauszufinden, welche Auswirkungen das Vorhandensein von Konstanten auf den Differenzierungsprozess hat. Dabei handelt es sich um Zahlen, die sich nicht ändern, wenn x oder y ihre Werte ändern.

Hinzugefügte Konstanten.

Beginnen wir mit dem einfachen Fall einer hinzugefügten Konstanten, also:

Sei y = x³ + 5.

Lassen Sie uns wie vorher auch annehmen, das x zu x + dx und y zu y + dy anwachsen werden.

Dann: y + dy = (x + dx)³ + 5
= x³ + 3x² dx + 3x(dx)² + (dx)sup>3 + 5.

Unter Vernachlässigung der Terme von höherer Ordnung wird dies zu

y + dy = x³ + 3x² · dx + 5.

Wenn wir das ursprüngliche y, d.h. y = x³ + 5 abziehen, bleibt das übrig:

dy = 3x² dx.
$\frac{dy}{dx} = 3x^2$.

Die Konstante, in diesem Fall die 5, ist verschwunden. Sie hat dem Wachstum von x nichts hinzugefügt und geht auch nicht in den Differentialkoeffizienten ein. Wenn wir 7, oder 700 oder eine andere Zahl anstelle von 5 gesetzt hätten, wäre auch diese verschwunden. Wenn wir also den Buchstaben a oder b oder c nehmen, um eine Konstante darzustellen, wird sie einfach verschwinden, wenn wir differenzieren.

Wenn die zusätzliche Konstante einen negativen Wert besitzt, so wie -5 oder -b, wird sie ebenfalls verschwinden. Unabhängig vom Vorzeichen verschwinden die Konstanten beim Differenzieren.

Multiplizierte Konstanten.

Nehmen Sie als einfaches Experiment diesen Fall:

Sei y = 7x².

Dann weiter wie bisher:

y + dy = 7(x+dx)²
= 7 (x² + 2x · dx + (dx)²)
= 7x² + 14x · dx + 7(dx)².

Subtrahieren Sie dann den ursprünglichen Term y = 7x², und vernachlässigen Sie den letzten Term, und wir erhalten

dy = 14x · dx.
$\frac{dy}{dx} = 14x$.

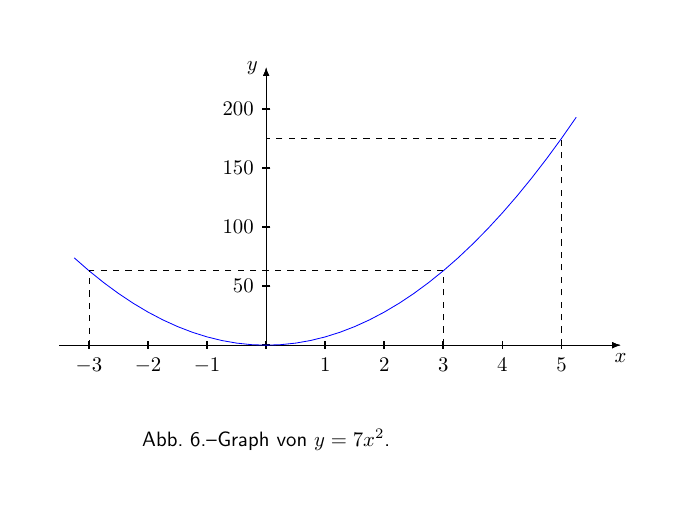
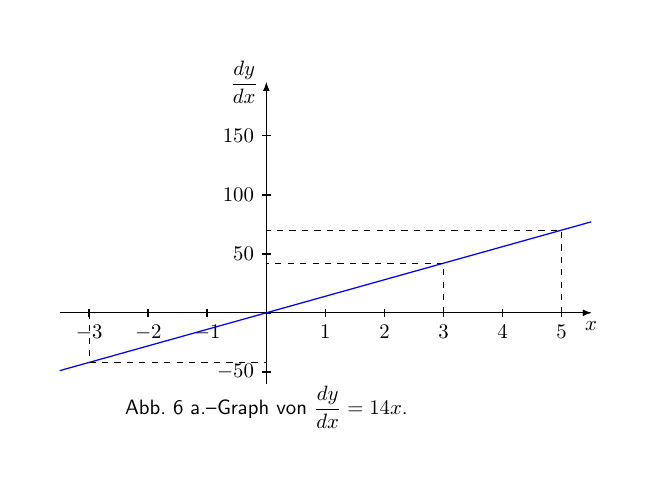
Lassen Sie uns dieses Beispiel dadurch veranschaulichen, dass wir die Graphen der Gleichungen y = 7x² und $\dfrac{dy}{dx} = 14x$ erstellen, indem wir x eine Reihe von aufeinanderfolgenden Werten zuweisen 0, 1, 2, 3, etc., und die entsprechenden Werte von y und von $\dfrac{dy}{dx}$ bestimmen.

Die so bestimmten Werte sind in der nachfolgenden Tabelle zusammengefasst:

x	0	1	2	3	4	5	-1	-2	-3
y	0	7	28	63	112	175	7	28	63
$\dfrac{dy}{dx}$	0	14	28	42	56	70	-14	-28	-42

Zeichnen Sie nun diese Werte, mit einer passenden Skala, und wir erhalten die beiden Kurven, Abbildung 6 und Abbildung 6a.

Vergleichen Sie die beiden Abbildungen sorgfältig und prüfen Sie durch Inaugenscheinnahme, ob die Höhe der Ordinate der abgeleiteten Kurve, Abb. 6a, proportional zur Steigung der ursprünglichen Kurve (siehe hier über die Steigung von Kurven.) Abbildung 6, bei dem entsprechenden Wert von x ist. Links vom Ursprung, wo die ursprüngliche Kurve negativ abfällt, sind die entsprechend den Ordinaten der abgeleiteten Kurve negativ.

Nun, wenn wir auf hier zurückblicken, werden wir sehen, dass differenzieren von x² uns 2x gibt. Sodass der Differentialkoeffizient von 7x² gerade 7 mal so groß ist wie der von x². Wenn wir 8x² genommen hätten, wäre der Differentialkoeffizient achtmal so groß gewesen wie der von x². Wenn wir y = ax² setzen, erhalten wir

\[ \frac{dy}{dx} = a \times 2x. \]

Wenn wir mit y = axⁿ begonnen hätten, hätten wir $\dfrac{dy}{dx} = a\times nx^{n-1}$ erhalten. Was nichts anderes bedeutet als, dass jede Multiplikation mit einer Konstanten, als bloße Multiplikation wieder auftaucht, wenn das Objekt differenziert wird. Und was für die Multiplikation wahr ist, gilt auch für die Division: Denn wenn wir im obigen Beispiel die Konstante $\frac{1}{7}$ anstelle von 7 genommen, hätten wir das gleiche $\frac{1}{7}$ im Ergebnis nach der Differenzierung erhalten.

Einige weitere Beispiel. Die folgenden Beispiele, die mit einer vollständigen Musterlösung abgearbeitet wurden, ermöglichen es ihnen, den Prozess der Differenzierung, wie er auf gewöhnliche algebraische Ausdrücke angewendet wird, vollständig zu beherrschen, und die am Ende dieses Kapitels angegebenen Beispiel selbst zu lösen.

(1) Differenzieren Sie $y = \dfrac{x^5}{7} - \dfrac{3}{5}$.

$\dfrac{3}{5}$ ist eine (zusätzliche) Konstante und verschwindet (siehe hier).

Wir können dann sofort schreiben

\[ \frac{dy}{dx} = \frac{1}{7} \times 5 \times x^{5-1}, \\ \text{bzw. }\; \frac{dy}{dx} = \frac{5}{7} x^4. \]

(2) Differenzieren Sie $y = a\sqrt{x} - \dfrac{1}{2}\sqrt{a}$.

Der Ausdruck (Term) $\dfrac{1}{2}\sqrt{a}$ verschwindet, da es eine Konstante ist; und wenn wir $a\sqrt{x}$ in der Potenzform als $ax^{\frac{1}{2}}$ schreiben, haben wir

\[ \frac{dy}{dx} = a \times \frac{1}{2} \times x^{\frac{1}{2}-1} = \frac{a}{2} \times x^{-\frac{1}{2}}, \\ \text{bzw. }\; \frac{dy}{dx} = \frac{a}{2\sqrt{x}}. \]

(3) Bestimmen Sie für $ay + bx = by - ax + (x+y) \sqrt{a^2 - b^2}$, den Differentialkoeffizienten von y in Bezug auf x.

In der Regel braucht ein solcher Ausdruck etwas mehr Wissen, als wir bisher erworben haben; es lohnt sich, jedoch immer zu versuchen, ob der Ausdruck in eine einfachere Form gebracht werden kann.

Zuerst müssen wir versuchen, den Ausdruck in die Form y =   zu bringen, sodass alle x auf einer Seite sind.

Der Ausdruck lässt sich wie folgt schreiben

\[ (a-b)y + (a + b)x = (x+y) \sqrt{a^2 - b^2}. \]

Quadrieren und wir erhalten

(a - b)² y² + (a + b)² x² + 2(a + b)(a - b)xy = (x² + y² + 2xy)(a² - b²),

was sich vereinfachen lässt zu

(a-b)²y² + (a + b)² x² = x²(a² - b²) + y²(a² - b²);
beziehungsweise
[(a-b)² - (a² - b²)] y² = [(a² - b ²) - (a + b)²] x²,
und das ist 2b(b - a)y² = -2b(b + a)x²;

Daraus folgt

\[ y = \sqrt{\frac{a+b}{a-b}} x \quad\text{und}\quad \frac{dy}{dx} = \sqrt{\frac{a+b}{a-b}}. \]

(4) Das Volumen eines Zylinders vom Radius r und der Höhe h ist durch die Formel V = π r² h gegeben. Bestimmen Sie die Rate der Volumenänderung in Abhängigkeit vom Radius, wenn r = 5,5 cm und h = 20 cm beträgt. Bestimmen Sie, wenn r = h ist, die Dimension des Zylinders, so dass eine Änderung um 1 cm im Radius zu einer Veränderung von 400 cm³ im Volumen führt.

Die Rate der Veränderung von V bezüglich r ist

\[ \frac{dV}{dr} = 2 \pi r h. \]

Wenn r = 5,5 cm und h = 20 cm sind ergibt sich für die Volumenänderung 2 π r h ≈ 691,15 cm³. Das bedeutet, dass die Veränderung des Radius um 1 cm zu einer Veränderung des Volumens von 691,15 cm³ führt. Das kann einfach überprüft werden, für r = 5 und r = 6 sind die Volumen 1570,8 cm³ beziehungsweise 2261,95 cm³ und die Differenz zwischen beiden beträgt 2261,95 – 1570,8 = 691,15.

Also wenn, \[ r=h,\quad \dfrac{dV}{dr} = 2\pi r^2 = 400\quad \text{und}\quad r = h = \sqrt{\dfrac{400}{2\pi}} \approx 7,98 \text{cm}. \]

(5) Mit Hilfe eines Strahlungspyrometers lässt sich die Temperatur eines Körpers messen, ohne diesen Körper zu berühren. Dazu wird ein Wert $\theta$ abgelesen, wobei dieser Wert von der Temperatur t in Grad Celsius des Körpers abhängt.

\[ \dfrac{\theta}{\theta_1} = \left(\dfrac{t}{t_1}\right)^4, \]

wobei $\theta_1$ der abgelesene Wert für eine bekannte Temperatur $t_1$ des betrachteten Körpers ist.

Vergleichen Sie die Empfindlichkeit des Pyrometers bei den Temperaturen 800°C., 1000°C., 1200°C., unter der Annahme, dass bei einer bekannten Temperatur von 1000°C der Wert 25 abgelesen wurde.

Die Empfindlichkeit ist die Rate der Veränderung der abgelesenen Messwerte in Abhängigkeit von der Temperatur, also $\dfrac{d\theta}{dt}$. Die Formel kann so geschrieben werden

\[ \theta = \dfrac{\theta_1}{t_1^4} t^4 = \dfrac{25t^4}{1000^4}, \]

und wir haben

\[ \dfrac{d\theta}{dt} = \dfrac{100t^3}{1000^4} = \dfrac{t^3}{10 000 000 000}. \]

Für t = 800, 1000 und 1200, erhalten $\dfrac{d\theta}{dt} = 0,0512$; 0,1 beziehungsweise 0,1728.

Zwischen 800° und 1000° verdoppelt sich die Empfindlichkeit fast, und wird bei 1200° nochmal größer um ca. drei Viertel.

Übung II

Differenzieren Sie die folgenden Ausdrücke:

(1) y = ax³ + 6.

(2) $y = 13x^{\frac{3}{2}} - c$.

(3) $y = 12x^{\frac{1}{2}} + c^{\frac{1}{2}}$. (4) $y = c^{\frac{1}{2}} x^{\frac{1}{2}}$.

(5) $u = \dfrac{az^n - 1}{c}$.

(6) y = 1,18t² + 22,4.

Stellen Sie sich einigen andere Beispiel zusammen und versuchen Sie, diese zu differenzieren.

(7) Wenn l_t und l₀ die Länge einer Stange aus Eisen, bei den Temperaturen t° C und 0° C sind, und es gilt, das l_t = l₀(1 + 0,000012t) ist. Bestimmen Sie die Längenänderung der Stange pro Grad Celsius.

(8) Es wurde festgestellt, dass die Leuchtleistung c einer Glühlampe sich durch c = aV^b beschreiben lässt. Wobei V die Spannung ist, und a und b Konstanten sind.

Ermitteln Sie, die Änderungsrate der Leuchtleistung in Abhängigkeit von der Spannung und berechnen Sie die Änderung der Leuchtleistung pro Volt für 80, 100 und 120 Volt bei einer Lampe für die a = 0,5 × 10^-10 und b = 6 gilt.

(9) Die Frequenz n der Vibration einer Saite (Schnur), die einen Durchmesser D, eine Länge L und ein spezifisches Gewicht σ besitzt, und die einer Kraft T gedehnt wird, ist gegeben durch

\[ n = \dfrac{1}{DL} \sqrt{\dfrac{gT}{\pi\sigma}}. \]

Bestimmen Sie die Änderungsrate der Frequenz, wenn D, L, σ und T einzeln varriert werden.

(10) Der größte äußere Druck P, den ein Rohr tragen kann, ohne zu zerbrechen, ist gegeben durch

\[ P = \left(\dfrac{2E}{1-\sigma^2}\right) \dfrac{t^3}{D^3}, \]

wobei E und σ Konstanten sind, t die Dicke des Rohres und D sein Durchmesser ist. (Diese Formel setzt Voraus, dass $4t$ im Vergleich zu D klein ist.)

Vergleichen Sie die Rate, mit der sich P verändert, wenn es Einzel betrachtet zu kleinen Änderungen der Dicke und kleinen Änderungen des Durchmessers kommt.

(11) Bestimmen Sie die Veränderungsrate, mit der sich bei einer Änderung des Radius Folgendes ändert:

(a) - der Umfang eines Kreises in Abh. von r;

(b) - die Fläche eines Kreises in Abh. von r;

(c) - die seitliche Fläche eines Kegels mit einer schrägen Dimension von l;

(d) - das Volumen eines Kegels mit Radius r und Höhe h;

(e) - die Fläche einer Kugel mit Radius r;

(f) - das Volumen einer Kugel mit Radius r.

(12) Die Länge L eines Eisenstabs wird, bei einer Temperatur T mit L = l_t[1 + 0,000012(T-t)] angegeben, wobei l_t die Länge bei der Temperatur t ist, ermitteln Sie die Variationsrate des Durchmessers des Eisenreifens, der auf ein Rad aufgezogen (geschrumpft) wird, wenn die Temperatur T variiert wird.

?

Antworten

(1) $\dfrac{dy}{dx} = 3ax^2$.

(2) $\dfrac{dy}{dx} = 13 \times \frac{3}{2}x^{\frac{1}{2}}$.

(3) $\dfrac{dy}{dx} = 6x^{-\frac{1}{2}}$.

(4) $\dfrac{dy}{dx} = \dfrac{1}{2}c^{\frac{1}{2}} x^{-\frac{1}{2}}$.

(5) $\dfrac{du}{dz} = \dfrac{an}{c} z^{n-1}$.

(6) $\dfrac{dy}{dt} = 2,36t$.

(7) $\dfrac{dl_t}{dt} = 0,000012\times l_0$.

(8) $\dfrac{dC}{dV} = abV^{b-1}$, 0,98, 3,00 und 7,47 Leuchtkraft beziehungsweise Leuchtkraft pro Volt.

(9) \[ \dfrac{dn}{dD} = -\dfrac{1}{LD^2} \sqrt{\dfrac{gT}{\pi \sigma}}, \dfrac{dn}{dL} = -\dfrac{1}{DL^2} \sqrt{\dfrac{gT}{\pi \sigma}}, \\ \dfrac{dn}{d \sigma} = -\dfrac{1}{2DL} \sqrt{\dfrac{gT}{\pi \sigma^3}}, \dfrac{dn}{dT} = \dfrac{1}{2DL} \sqrt{\dfrac{g}{\pi \sigma T}}. \]

(10) \[ \dfrac{\text{Die Veränderungsrate von P wenn t sich verändert}} {\text{Die Veränderungsrate von P, wenn D sich verändert}} = - \dfrac{D}{t} \]

(11) 2π, 2π r, π l, 2⁄3 π rh, 8π r, 4π r².

(12) $\dfrac{dD}{dT} = \dfrac{0,000012l_t}{\pi}$.