Über relatives Wachstum

Im gesamten Calculus haben wir es mit Mengen zu tun, die wachsen, und mit Wachstumsraten. Wir teilen alle Größen in zwei Klassen ein: Konstanten und Variablen. Diejenigen, die wir als von festem Wert betrachten und Konstanten nennen, bezeichnen wir im Allgemeinen algebraisch mit Buchstaben vom Anfang des Alphabets, wie a, b oder c; während diejenigen, die wir als wachsend oder (wie die Mathematiker sagen) als veränderlich betrachten, bezeichnen wir mit Buchstaben vom Ende des Alphabets, wie x, y, z, u, v, w, oder manchmal t.

Außerdem haben wir es meist mit mehr als einer Variablen gleichzeitig zu tun und denken an die Art und Weise, wie eine Variable von der anderen abhängt: Zum Beispiel denken wir an die Art und Weise, wie die von einem Projektil erreichte Höhe von der Zeit abhängt, in der es diese Höhe erreicht. Oder wir werden aufgefordert, ein Rechteck mit gegebener Fläche zu betrachten und zu fragen, wie eine Vergrößerung der Länge eine entsprechende Verkleinerung der Breite erzwingt. Oder wir denken an die Art und Weise, wie jede Veränderung der Neigung einer Leiter die Höhe, die sie erreicht, variieren lässt.

Angenommen, wir haben zwei solcher Variablen, die voneinander abhängen. Eine Änderung der einen führt zu einer Änderung der anderen, wegen dieser Abhängigkeit. Nennen wir eine der Variablen x, und die andere, die von ihr abhängt, y.

Angenommen, wir bringen x dazu, zu variieren, das heißt, wir verändern es oder stellen uns vor, dass es verändert wird, indem wir zu ihm ein Teil hinzufügen, das wir dx nennen. Wir bewirken also, dass x zu x + dx wird. Dann, weil x verändert wurde, hat sich auch y verändert und ist zu y + dy geworden. Hier kann das Teil dy in einigen Fällen positiv, in anderen negativ sein; und es wird in dem meisten Fällen nicht die gleiche Größe wie dx haben.

Zwei Beispiele.

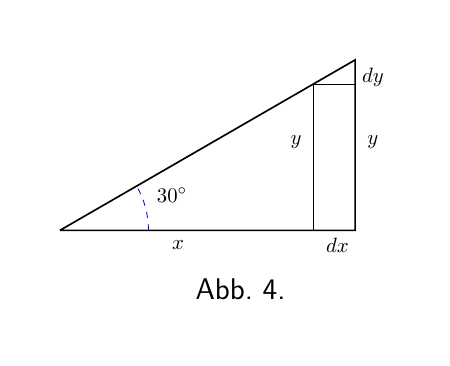
(1) Seien x und y die Basis beziehungsweise die Höhe eines rechtwinkligen Dreiecks (Abbildung 4), die Neigung der dritten Seite sei auf 30° festgelegt ist. Wenn wir annehmen, dass sich dieses Dreieck ausdehnt und dennoch seine Winkel gleich bleiben, dann wird, wenn die Basis so wächst, dass sie x + dx wird, die Höhe zu y + dy. Hier führt die Vergrößerung von x zu einer Vergrößerung von y. Das kleine Dreieck, dessen Höhe dy und dessen Basis dx ist, ähnelt dem ursprünglichen Dreieck; und es ist offensichtlich, dass der Wert des Verhältnisses $\dfrac{dy}{dx}$ der gleiche ist wie der des Verhältnisses $\dfrac{y}{x}$. Da der Winkel 30° ist, wird man sehen, dass hier:

\[ \frac{dy}{dx} = \frac{1}{1,73} \]

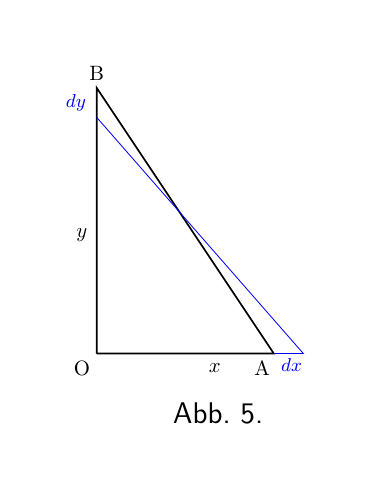
(2) Sei x in Abbildung 5 der horizontale Abstand (= Strecke OA) des unteren Endes einer Leiter fester Länge AB von einer Wand; und sei y die Höhe (= Strecke OB), die sie an der Wand erreicht. Nun hängt y eindeutig von x ab. Es ist leicht, zu sehen, dass, wenn wir das untere Ende A etwas weiter von der Wand wegziehen, das obere Ende B etwas tiefer herunterkommt. Lassen Sie uns dies in wissenschaftlicher Sprache ausdrücken. Wenn wir x auf x + dx erhöhen, dann wird y zu y - dy; das heißt, wenn x eine positive Erhöhung erhält, ist die Erhöhung, die zu y führt, negativ.

Ja, aber wie viel? Nehmen wir an, die Leiter sei so lang, dass, wenn das untere Ende A 3 m von der Wand entfernt ist, das obere Ende B 4 m vom Boden entfernt ist. Wenn Sie nun das untere Ende 1 cm weiter herausziehen würden, um wie viel würde das obere Ende herunterkommen? Geben Sie das Ganze in cm an: x = 300 cm, y = 400 cm. Das Inkrement von x, das wir dx nennen, beträgt nun 1 cm: oder x + dx = 301 cm.

Wie stark wird y verkleinert? Die neue Höhe wird y - dy sein. Wenn wir die Höhe mit dem Satz des Pythagoras ausrechnen, dann können wir herausfinden, wie viel dy sein wird. Die Länge der Leiter ist

\[ \sqrt{ (400)^2 + (300)^2 } = 500 \text{ cm}. \]

Die neue Höhe, die y - dy ist, ist dann so, dass

\begin{align*} (y - dy)^2 &= (500)^2 - (301)^2 = 250000 - 90601 = 159399, \\ y - dy &= \sqrt{159399} = 399,25 \text{cm}. \end{align*}

Nun ist y 400, so dass dy 400 - 399,25 = 0,75 cm beträgt.

Wir sehen also, dass die Erhöhung von dx um 1 cm eine Verringerung von dy um 0,75 cm zur Folge hat.

Und das Verhältnis von dy zu dx kann so angegeben werden:

\[ \frac{dy}{dx} = - \frac{0,75}{1}. \]

Es ist auch leicht, zu sehen, dass (außer an einer bestimmten Stelle) dy eine andere Größe als dx hat.

Jetzt sind wir quer durch die Differentialrechnung auf der Jagd nach einem merkwürdigen Ding, einem bloßen Verhältnis, nämlich dem Verhältnis, das dy zu dx hat, wenn beide unendlich klein sind.

Es sei an dieser Stelle angemerkt, dass wir dieses Verhältnis $\dfrac{dy}{dx}$ nur finden können, wenn y und x in irgendeiner Beziehung zueinanderstehen, so dass, wann immer x variiert, auch y variiert. So wird z. B. im ersten Beispiel, wenn die Basis x des Dreiecks verlängert wird, auch die Höhe y des Dreiecks größer, und im zweiten Beispiel, wenn der Abstand x des Fußes der Leiter von der Wand vergrößert wird, nimmt die von der Leiter erreichte Höhe y in entsprechender Weise ab, zunächst langsam, dann aber immer schneller, je größer x wird. In diesen Fällen ist die Beziehung zwischen x und y vollkommen eindeutig, sie kann mathematisch ausgedrückt werden, nämlich $\dfrac{y}{x} = \tan 30^{\circ}$ bzw. $x^2 + y^2 = l^2$ (wobei l die Länge der Leiter ist), und $\dfrac{dy}{dx}$ hat die Bedeutung, die wir in jedem Fall gefunden haben.

Wenn x wie bisher der Abstand des Leiterfußes von der Wand ist, y aber statt der erreichten Höhe die horizontale Länge der Wand oder die Anzahl der Steine in ihr oder die Anzahl der Jahre seit ihrem Bau ist, so würde jede Änderung von x natürlich keinerlei Änderung von y bewirken; in diesem Fall hat $\dfrac{dy}{dx}$ keinerlei Bedeutung, und es ist nicht möglich, einen Ausdruck dafür zu finden. Wann immer wir die Differentiale dx, dy, $dz$ usw. verwenden, wird die Existenz einer Art von Beziehung zwischen x, y, z usw, impliziert, und diese Beziehung nennt man eine "Funktion" in x, y, z, usw.; die beiden oben angegebenen Ausdrücke, nämlich $\dfrac{y}{x} = \tan 30^{\circ}$ und x² + y² = l², sind beispielsweise Funktionen von x und y. Solche Ausdrücke enthalten implizit (d. h. ohne es deutlich zu zeigen) die Möglichkeit, entweder x in Termen von y oder y in Termen von x auszudrücken, und werden deshalb implizite Funktionen in x und y genannt, sie können jeweils in die Formen gebracht werden

\begin{align*} y &= x \tan 30^\circ{} \quad\text{oder}\quad x = \frac{y}{\tan 30^\circ{}} \\ \text{und}\; y &= \sqrt{ l^2 - x^2} \quad\text{oder}\quad x = \sqrt{ l^2 - y^2}. \end{align*}

Diese letzten Ausdrücke geben explizit (also eindeutig) den Wert von x in Bezug auf y oder von y in Bezug auf x an und werden deshalb explizite Funktionen von x oder y genannt. Zum Beispiel ist x² + 3 = 2y - 7 eine implizite Funktion in x und y; sie kann geschrieben werden, als $y = \dfrac{x^2 + 10}{2}$ (explizite Funktion von x) oder $x = \sqrt{2y - 10}$ (explizite Funktion von y). Wir sehen, dass eine explizite Funktion von x, y, z usw. einfach etwas ist, dessen Wert sich ändert, wenn sich x, y, z usw. ändern, entweder einzeln oder mehrere zusammen. Deshalb nennt man den Wert der expliziten Funktion abhängige Variable, der vom Wert der anderen variablen Größen in der Funktion abhängt; diese anderen Variablen nennt man die unabhängigen Variablen, weil ihr Wert nicht von dem Wert bestimmt wird, den die Funktion annimmt. Ist beispielsweise $u = x^2 \sin \theta$, so sind x und $\theta$ die unabhängigen Variablen und u ist die abhängige Variable.

Manchmal ist die genaue Beziehung zwischen mehreren Größen x, y, z entweder nicht bekannt oder es ist nicht bequem, sie anzugeben; es ist dennoch möglich, anzugeben, dass es eine Art Beziehung zwischen diesen Variablen gibt, auch wenn man weder x noch y oder z einzeln ändern kann, ohne die anderen Größen zu beeinflussen; die Existenz einer Funktion in x, y, z wird dann durch die Notation F(x, y, z) (implizite Funktion) oder durch x = F(y, z), y = F(x, z ) oder z = F(x, y) (explizite Funktion) angegeben. Manchmal wird anstelle von F der Buchstabe f oder φ verwendet, so dass $y = F(x)$, $y = f(x)$ und $y = \phi(x)$ wobei alle Schreibweisen dasselbe bedeuten, nämlich dass der Wert von y in irgendeiner nicht angegebenen Weise vom Wert von x abhängt.

Das Verhältnis $\dfrac{dy}{dx}$ nennen wir den Differentialkoeffizienten von y bezüglich x. Das ist ein feierlicher wissenschaftlicher Name für diese sehr einfache Sache. Aber wir werden uns nicht von feierlichen Namen erschrecken lassen, wenn die Dinge selbst so einfach sind. Statt uns zu erschrecken, werden wir einfach einen kurzen Fluch über die Dummheit aussprechen, lange, knackige Namen zu vergeben; und, nachdem wir unser Gemüt erleichtert haben, werden wir zu dem einfachen Ding selbst übergehen, nämlich dem Verhältnis $\dfrac{dy}{dx}$.

In der gewöhnlichen Algebra, die Sie in der Schule gelernt haben, waren Sie immer auf der Jagd nach irgendeiner unbekannten Größe, die Sie x oder y nannten; oder manchmal waren es zwei unbekannte Größen, nach denen gleichzeitig gejagt wurde. Sie müssen nun lernen, auf eine neue Art und Weise zu jagen; der Fuchs ist nun weder x noch y. Stattdessen müssen Sie nach diesem merkwürdigen Objekt namens $\dfrac{dy}{dx}$ jagen. Der Vorgang, den Wert von $\dfrac{dy}{dx}$ zu finden, heißt Differenzieren. Aber denken Sie daran: Gesucht ist der Wert dieses Verhältnisses, wenn sowohl dy als auch dx selbst sind unendlich klein. Der wahre Wert des Differentialkoeffizienten ist derjenige, dem er sich im Grenzfall annähert, wenn jedes von ihnen als unendlich klein betrachtet wird.

Lernen wir nun, wie man auf die Suche nach $\dfrac{dy}{dx}$ geht.

Hinweise zu Kapitel III.

Wie man Differentiale liest.

Niemals wird man in den Schuljungenfehler verfallen, zu denken, dx bedeute d mal x, denn d ist kein Faktor, sondern bedeutet ein Element von oder ein Stück von, was immer folgt. Man liest dx also: "dee-iks."

Für den Fall, dass der Leser niemanden hat, der ihn in solchen Dingen anleitet, sei hier einfach gesagt, dass man Differentialkoeffizienten auf folgende Weise liest. Der Differentialkoeffizient

$\dfrac{dy}{dx}$

als dee-ypsilon durch dee-iks oder als dee-ypsilion über dee-iks gelesen. Und entsprechend wird

$\dfrac{du}{dt}$ als dee-uh durch dee-tee gelesen.

Sekundäre Differentialkoeffizienten werden wir später kennenlernen. Sie lauten so: $\dfrac{d^2 y}{dx^2};$ Das heißt "dee-zwei-ypsilion über dee-iks-quadrat" und bedeutet, dass die Operation des Differenzierens von y nach x zweimal durchgeführt wurde (oder werden muss).

Eine weitere Möglichkeit, anzuzeigen, dass eine Funktion differenziert wurde, besteht darin, einen Akzent auf das Symbol der Funktion zu setzen. Wenn also $y=F(x)$, bedeutet, dass y eine nicht spezifizierte Funktion von x ist (siehe hier), können wir F′(x) statt $\dfrac{d\bigl(F(x)\bigr)}{dx}$ schreiben. Analog dazu bedeutet F′′(x), dass die ursprüngliche Funktion F(x) zweimal nach x differenziert wurde.

Einfachste Fälle

Nun wollen wir sehen, wie wir nach ersten Prinzipien einige einfache algebraische Ausdrücke differenzieren können.

Fall 1

Lassen Sie uns mit dem einfachen Ausdruck y = x² beginnen. Erinnern wir uns daran, dass der fundamentale Begriff des Calculus die Idee des Wachsens ist. Mathematiker bezeichnen es als variieren. Da nun y und x² einander gleich sind, ist klar, dass, wenn x wächst, auch x² wächst. Und wenn x² wächst, dann wird auch y wachsen. Was wir herausfinden müssen, ist das Verhältnis zwischen dem Wachstum von y und dem Wachstum von x. Mit anderen Worten: Unsere Aufgabe ist es, das Verhältnis zwischen dy und dx herauszufinden, oder, kurz gesagt, den Wert von $\dfrac{dy}{dx}$ zu bestimmen.

Lassen Sie x also ein wenig größer werden und x + dx werden; ebenso wird y ein wenig größer werden und y + dy werden. Dann stimmt es natürlich immer noch, dass das vergrößerte y gleich dem Quadrat des vergrößerten x sein wird. Wenn wir das aufschreiben, haben wir:

\begin{align*} y + dy &= (x + dx)^2.\\ \text{Wenn wir den quadratischen }\\ \text{Ausdruck auflösen erhalten wir:}\;\\ y + dy &= x^2 + 2x \cdot dx+(dx)^2. \end{align*}

Was bedeutet (dx)²? Erinnern Sie sich, dass dx ein bisschen - ein kleines bisschen - von x bedeutet. Dann bedeutet (dx)² ein bisschen eines kleines Bisschen von x; das heißt, wie oben (hier) erklärt, ist es eine kleine Menge zweiter Ordnung der Kleinheit. Sie kann daher als ziemlich unbedeutend im Vergleich zu den anderen Termen verworfen werden. Lässt man ihn weg, so ergibt sich:

y + dy = x² + 2x · dx
Mit y = x²;Subtrahieren wir das von der Gleichung und haben das übrig
dy = 2x · dx
Dividieren durch dx, und wir haben
$\frac{dy}{dx} = 2x$.

Nun das* ist das, was wir zu finden versuchen. Das Verhältnis des Wachstums von y zum Wachstum von x beträgt im vorliegenden Fall 2x.

*Anmerkung: Dieses Verhältnis $\dfrac{dy}{dx}$ ist das Ergebnis der Differenzierung von y nach x. Differenzieren bedeutet, den Differentialkoeffizienten zu finden. Nehmen wir an, wir hätten eine andere Funktion von x, wie z. B. u = 7x² + 3. Wenn wir dann aufgefordert würden, diese nach x zu differenzieren, müssten wir $\dfrac{du}{dx}$ finden, oder, was dasselbe ist, $\dfrac{d(7x^2 + 3)}{dx}$. Andererseits können wir einen Fall haben, in dem die Zeit die unabhängige Variable ist (siehe hier), wie zum Beispiel: $y = b + \frac{1}{2} at^2$. Wenn wir diesen Ausdruck dann differenzieren sollen, bedeutet das, dass wir seinen Differentialkoeffizienten bezüglich t finden müssen. Unsere Aufgabe wäre es dann, $\dfrac{dy}{dt}$ zu finden, also $\dfrac{d(b + \frac{1}{2} at^2)}{dt}$.

Numerisches Beispiel.

Angenommen, x = 100 und daher ist y = 10000. Dann lasse man x wachsen, bis es 101 wird (d.h. dx = 1). Dann wird das vergrößerte y 101 × 101 = 10201 sein. Wenn wir uns aber darauf einigen, dass wir kleine Mengen zweiter Ordnung ignorieren dürfen, kann 1 gegenüber 10000 verworfen werden; wir können also das vergrößerte y auf 10200 abrunden. y ist von 10000 auf 10200 angewachsen; das hinzugefügte Teil ist dy, das also 2 beträgt.

$\dfrac{dy}{dx} = \dfrac{200}{1} = 200$. Nach der Algebra-Arbeit des vorherigen Abschnitts finden wir $\dfrac{dy}{dx} = 2x$. Und so ist es, wenn wir für x = 100 setzen folgt daraus, das 2x = 200 ist.

Aber, werden Sie sagen, wir haben doch eine ganze Einheit vernachlässigt.

Nun, versuchen Sie es noch einmal, indem Sie dx noch ein bisschen kleiner machen. Anstelle davon, dass wir x um 1 Vergrößern, versuchen wir es diesmal mit $dx=\frac{1}{10}$. Dann ist x + dx = 100,1, und

(x + dx)² = 100,1 × 100,1 = 10020,01.

Nun ist die letzte Zahl 1 nur ein millionstel Teil der 10 000, und ist völlig vernachlässigbar; wir können also 10020 ohne das kleine Komma am Ende nehmen. Und das ergibt dy = 20 und $\dfrac{dy}{dx} = \dfrac{20}{0.1} = 200$, was immer noch das Gleiche ist wie 2x.

Fall 2

Versuchen Sie, y = x³ auf die gleiche Weise zu differenzieren.

Wir lassen y auf y + dy anwachsen, während x auf x + dx anwächst.

Dann haben wir

y + dy = (x + dx)³.

Denn kubischen Ausdruck auflösen und wir erhalten

y + dy = x³ + 3x² · dx + 3x(dx)²+(dx)³.

Nun wissen wir, dass wir kleine Mengen zweiter und dritter Ordnung vernachlässigen dürfen; denn wenn dy und dx beide sehr (sehr) klein gemacht werden, werden (dx)² und (dx)³ im Vergleich dazu unendlich klein. Betrachten wir sie also als vernachlässigbar, so bleibt übrig:

y + dy = x³ + 3x² · dx.

y = x³; und wenn wir das Subtrahieren erhalten wir:

dy = 3x² · dx,
und
$\frac{dy}{dx}$ = 3x².

Fall 3

Versuchen Sie, y = x⁴ zu differenzieren. Indem wir wie zuvor sowohl y als auch x ein wenig wachsen lassen, haben wir:

y + dy = (x + dx)⁴.

Wenn wir die Erhöhung zur vierten Potenz ausrechnen, erhalten wir

y + dy = x⁴ + 4x³ dx + 6x²(dx)² + 4x(dx)³+(dx)⁴.

Streichen wir dann die Terme, die alle höheren Potenzen von dx enthalten, da sie im Vergleich vernachlässigbar sind, so haben wir

y + dy = x⁴ + 4x³ dx.

Subtrahieren wir den ursprüngliche Ausdruck y = x⁴, so haben wir links

dy = 4x³ dx,
und $\frac{dy}{dx} = 4x^3$.

Nun sind alle diese Fälle recht einfach. Lassen Sie uns die Ergebnisse sammeln, um zu sehen, ob wir eine allgemeine Regel ableiten können. Legen Sie sie in zwei Spalten, die Werte von y in die eine und die entsprechenden für $\dfrac{dy}{dx}$ gefundenen Werte in die andere: also

y	$\frac{dy}{dx}$
x2	2x
x3	3x2
x4	4x3

Schauen Sie sich diese Ergebnisse an: Die Operation des Differenzierens scheint den Effekt zu haben, die Potenz von x, um 1 zu verkleinern (zum Beispiel im letzten Fall x⁴ auf x³ zu reduzieren) und gleichzeitig mit einer Zahl zu multiplizieren (und zwar mit derselben Zahl, die ursprünglich als Potenz erschien). Wenn Sie das einmal gesehen haben, können Sie leicht vermuten, wie die anderen Fälle ablaufen werden. Sie würden erwarten, dass das Differenzieren von x⁵ 5x⁴ ergibt, oder das Differenzieren von x⁶ 6x⁵. Wenn Sie zögern, probieren Sie eine davon aus und schauen Sie, ob die Vermutung richtig ist.

Versuchen Sie y = x⁵.

dann y + dy = (x + dx)⁵
= x⁵ + 5x⁴ dx + 10x³(dx)² + 10x²(dx)³ + 5x(dx)⁴ + (dx)⁵.

Vernachlässigen wir alle Terme, die kleine Mengen höherer Ordnungen enthalten, so bleiben

y + dy = x⁵ + 5x⁴ dx,
und subtrahieren y = x⁵ und erhalten
dy = 5x⁴ dx,
dann $\frac{dy}{dx} = 5x^4$, genau wie wir angenommen haben.

Wenn wir unsere Beobachtung logisch weiterverfolgen, sollten wir zu dem Schluss kommen, dass wir, wenn wir mit einer beliebigen höheren Potenz - nennen wir sie n - umgehen wollen, dies auf die gleiche Weise tun können.

Wenn y = xⁿ ist

Dann sollten wir erwarten, dass

$\frac{dy}{dx} = nx^{(n-1)}$.

Beispielsweise sei n = 8, dann sei y = x⁸; und das Differenzieren würde $\dfrac{dy}{dx} = 8x^7$ ergeben.

Und in der Tat gilt die Regel, dass das Differenzieren von xⁿ als Ergebnis nx^n-1 ergibt, für alle Fälle, in denen n eine ganze Zahl und positiv ist. Die Erweiterung von (x + dx)ⁿ durch den binomischen Satz zeigt dies sofort. Aber die Frage, ob diese Regel auch für Fälle gilt, in denen n negative oder gebrochene Werte hat, erfordert weitere Überlegungen.

Im Fall einer negativen Potenz.

Sei y = x^-2. Dann verfahren Sie wie zuvor:

y + dy = ( x + dx)^-2
$= x^{-2} \left(1 + \frac{dx}{x}\right)^{-2}$.

Erweitert man dies durch den binomischen Lehrsatz (siehe hier), so erhält man

\begin{align*} &=x^{-2} \left[1 - \frac{2\, dx}{x} + \frac{2(2+1)}{1\times 2} \left(\frac{dx}{x}\right)^2 - \text{etc.}\right] \\ &=x^{-2} - 2x^{-3} \cdot dx + 3x^{-4}(dx)^2 - 4x^{-5}(dx)^3 + \text{etc.} \\ \end{align*}

So haben wir unter Vernachlässigung der kleinen Mengen höherer Ordnungen:

y + dy = x^-2 - 2x^-3 · dx.

Subtrahieren wir den ursprünglichen Ausdruck y = x^-2, so finden wir

dy = -2x^-3dx,
$\frac{dy}{dx} = -2x^{-3}$.

Und das ist immer noch in Übereinstimmung mit der oben hergeleiteten Regel.

Im Fall einer gebrochenen Potenz.

Sei $y= x^{\frac{1}{2}}$. Dann, wieder wie zuvor,

y + dy = (x+dx)^½ = x^½ $(1 + \frac{dx}{x} )^{\frac{1}{2}}$
$= \sqrt{x} + \frac{1}{2} \frac{dx}{\sqrt{x}} - \frac{1}{8} \frac{(dx)^2}{x\sqrt{x}} + $ Terme mit höheren Potenzen von dx.

Zieht man das ursprüngliche, $y = x^{\frac{1}{2}}$, ab und vernachlässigt die höheren Potenzen, so bleibt folgendes übrig:

\[ dy = \frac{1}{2} \frac{dx}{\sqrt{x}} = \frac{1}{2} x^{-\frac{1}{2}} \cdot dx, \] und $\dfrac{dy}{dx} = \dfrac{1}{2} x^{-\frac{1}{2}}$.

Der allgemeinen Regel wird entsprochen.

Zusammenfassung. Schauen wir, wie weit wir gekommen sind. Wir sind zu folgender Regel gelangt: Um xⁿ zu differenzieren, multipliziere mit der Potenz und reduziere die Potenz um eins, so dass wir nx^n-1 als Ergebnis erhalten.

Übungen I

Differenzieren Sie die folgenden Ausdrücke:

(1) y = x¹³

(2) $y = x^{-\frac{3}{2}}$

(3) y = x^2a

(4) u = t^{2,4}

(5) $z = \sqrt[3]{u}$

(6) $y = \sqrt[3]{x^{-5}}$

(7) $u = \sqrt[5]{\dfrac{1}{x^8}}$

(8) y = 2x^a

(9) $y = \sqrt[q]{x^3}$

(10) $y = \sqrt[n]{\dfrac{1}{x^m}}$

Sie haben nun gelernt, wie man Potenzen von x differenziert. Das ist einfach!

Antworten

(1) $\dfrac{dy}{dx} = 13x^{12}$.

(2) $\dfrac{dy}{dx} = - \dfrac{3}{2} x^{-\frac{5}{2}}$.

(3) $\dfrac{dy}{dx} = 2ax^{(2a-1)}$.

(4) $\dfrac{du}{dt} = 2,4t^{1,4}$.

(5) $\dfrac{dz}{du} = \dfrac{1}{3} u^{-\frac{2}{3}}$.

(6) $\dfrac{dy}{dx} = -\dfrac{5}{3}x^{-\frac{8}{3}}$.

(7) $\dfrac{du}{dx} = -\dfrac{8}{5}x^{-\frac{13}{5}}$.

(8) $\dfrac{dy}{dx} = 2ax^{a-1}$.

(9) $\dfrac{dy}{dx} = \dfrac{3}{q} x^{\frac{3-q}{q}}$.

(10) $\dfrac{dy}{dx} = -\dfrac{m}{n} x^{-\frac{m+n}{n}}$.