Über die verschiedene Grade der Kleinheit

Wir werden feststellen, dass wir es in unseren Rechenprozessen mit kleinen Mengen mit verschieden Graden der Kleinheit zu tun haben.

Wir werden auch lernen müssen, unter welchen Umständen wir kleine Mengen als so winzig betrachten können, dass wir sie aus der Betrachtung ausschließen können. Alles hängt von der relativen Winzigkeit ab.

Bevor wir irgendwelche Regeln festlegen, lassen Sie uns an einige bekannte Fälle denken. Es gibt 60 Minuten in der Stunde, 24 Stunden im Tag, 7 Tage in der Woche. Es gibt also 1440 Minuten am Tag und 10080 Minuten in der Woche.

Natürlich ist 1 Minute eine sehr kleine Zeitmenge im Vergleich zu einer ganzen Woche. In der Tat betrachteten unsere Vorfahren sie als klein im Vergleich zu einer Stunde und nannten sie eine mimùte, was einen winzigen Bruchteil - nämlich ein Sechzigstel - einer Stunde bedeutet. Als sie kamen, um noch kleinere Unterteilungen der Zeit zu verlangen, teilten sie jede Minute in 60 noch kleinere Teile, die sie in den Tagen von Königin Elisabeth zweite minùtes (d.h.: kleine Mengen der zweiten Ordnung der Minutenzahl) nannten. Heutzutage nennen wir diese kleinen Mengen der zweiten Ordnung der Kleinheit Sekunden. Aber nur wenige Menschen wissen, warum sie so genannt werden. Die Bezeichnung Sekunde leitet sich vom lateinischen Ausdruck pars minuta secunda ab, was der zum zweiten Mal verminderte Teil bedeutet.

Wenn nun eine Minute im Vergleich zu einem ganzen Tag so klein ist, wie viel kleiner ist dann im Vergleich dazu eine Sekunde!

Vergleichen Sie eine 1 Cent Münze mit einem 10 Euro Schein: Sie ist nur $\frac{1}{1000}$ der Banknote wert. Eine 1 Cent Münze ist im Vergleich zu einem 10 Euro Schein mehr oder weniger wenig wert: Sie kann durchaus als eine kleine Menge betrachtet werden. Aber wenn Sie jetzt die 1 Cent mit einem 500 Euro Schein vergleichen, erkennen Sie, das die Münze keine Bedeutung besitzt, obwohl sie dem $\frac{1}{1000}$ Teil eines 10 Euro Scheines entspricht. Selbst ein 500 Euro Schein eine relativ vernachlässigbare Größe im Vermögen eines Millionärs.

Wenn wir nun irgendeinen numerischen Bruchteil als den Anteil festlegen, den wir für irgendeinen Zweck als relativ klein bezeichnen, so können wir leicht andere Brüche von höherem Grad der Kleinheit angeben. Wenn also $\frac{1}{60}$ für den Zweck der Zeit ein kleiner Bruchteil genannt wird, dann kann $\frac{1}{60}$ von $\frac{1}{60}$ (als ein kleiner Bruchteil eines kleinen Bruches) als eine kleine Menge zweiter Ordnung der Kleinheit betrachtet werden. *

*Die Mathematiker sprechen von der zweiten Ordnung der Größe, auch wenn sie eigentlich die zweite Ordnung der Kleinheit meinen. Das ist für Anfänger sehr verwirrend.

Oder, wir betrachten 1 Prozent (d.h.: $\frac{1}{100}$) als einen kleinen Bruch, dann ist 1 Prozent von 1 Prozent. (d.h.: $\frac{1}{10.000}$) ein kleiner Bruchteil zweiter Ordnung der Kleinheit; und $\frac{1}{1.000.000}$ wäre ein kleiner Bruchteil dritter Ordnung der Kleinheit, nämlich 1 Prozent von 1 Prozent von 1 Prozent von 1 Prozent.

Letzten Endes nehmen wir an, dass wir für irgendeinen sehr genauen Zweck $\frac{1}{1.000.000}$ als klein betrachten sollten. Wenn also eine erstklassige Uhr in einem Jahr nicht mehr als eine halbe Minute verlieren oder gewinnen soll, muss er die Zeit mit einer Genauigkeit von 1 Teil in 1.051.200 halten. Wenn wir nun für einen solchen Zweck $\frac{1}{1.000.000}$ (oder ein Millionstel) als eine kleine Menge betrachten, dann ist $\frac{1}{1.000.000}$ von $\frac{1}{1.000.000}$, also $\frac{1}{1, 000.000.000.000}$ (oder ein Billionstel) eine kleine Menge zweiter Ordnung und kann im Vergleich dazu völlig vernachlässigt werden.

Dann sehen wir, dass je kleiner eine kleine Menge selbst ist, desto vernachlässigbarer wird die entsprechende kleine Menge zweiter Ordnung. Daher wissen wir, dass wir in allen Fällen berechtigt sind, die kleinen Mengen zweiter oder dritter (oder höherer) Ordnung zu vernachlässigen, wenn wir nur die kleine Menge erster Ordnung in sich selbst klein genug nehmen.

Ob eine Betrachtung beziehungsweise die Berücksichtigung einer Größe von Bedeutung ist hängt auch von dem Kontext in dem sie verwendet wird ab. Um dafür ein besseres Gespür zu entwickeln betrachten wir die Ergebnisse der olympischen Spiele 2020 in Tokyo. Die Siegerin hat beim 20 km Gehen 1:29:12 (also 1 Stunde 29 Minuten und 12 Sekunden) für die Strecke benötigt. Beim 1500 Meter Lauf benötigte die Siegerin 3:53,11 Minuten (also 3 Minuten 53 Sekunden und 11 hundertstel Sekunden).

Beim ersten Beispiel waren Sekunden noch ausreichend während beim zweiten Beispiel bereits hundertstel Sekunden für die Beschreibung benötigt werden. Mit anderen Worten während beim 1500 Meter Lauf hundertstel Sekunden betrachtet werden können diese beim 20 km Gehen vernachlässigt werden.

Aber es ist zu bedenken, dass kleine Mengen, wenn sie in unseren Ausdrücken als Faktoren multipliziert mit einem anderen Faktor auftreten, wichtig werden können, wenn der andere Faktor selbst groß ist. Selbst ein Cent wird wichtig, wenn er nur mit ein paar Hundert multipliziert wird.

In der Infinitesimalrechnung schreiben wir dx für ein kleines Stückchen x. Diese Dinge wie dx und du und dy nennt man Differentiale, das Differential von x, oder von u, oder von y, je nachdem. (Man liest sie als dee-iks, oder dee-u, oder dee-y.) Wenn dx ein kleines Stück von x ist, und zwar ein relativ kleines, so folgt daraus nicht, dass solche Größen wie x · dx, oder x² dx, oder a^x dx vernachlässigbar sind. Aber dx × dx wäre vernachlässigbar, da es eine kleine Menge zweiter Ordnung ist.

Ein sehr einfaches Beispiel soll zur Veranschaulichung dienen.

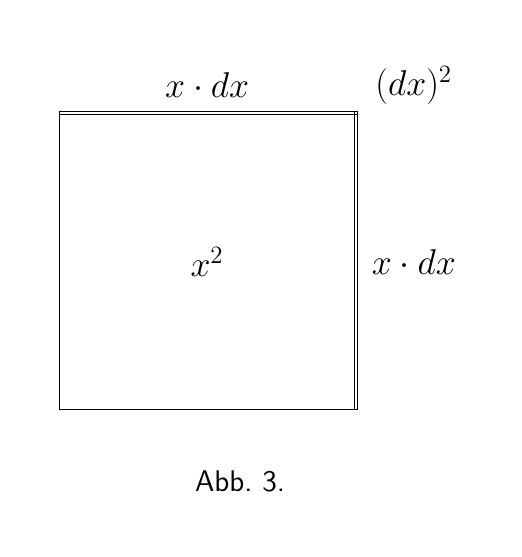
Stellen wir uns x als eine Menge vor, die um einen kleinen Betrag wachsen kann, so dass sie zu x + dx wird, wobei dx der kleine Zuwachs ist, der durch das Wachstum entsteht. Das Quadrat hiervon ist x² + 2x · dx + (dx)². Der zweite Term ist nicht vernachlässigbar, weil er eine Größe erster Ordnung ist; während der dritte Term von der zweiten Ordnung der Kleinheit ist, nämlich ein bisschen von x². Wenn wir also dx als numerischen Wert, sagen wir, $\frac{1}{60}$ von x auffassen, dann wäre der zweite Term $\frac{2}{60}$ von x², während der dritte Term $\frac{1}{3600}$ von x² wäre. Dieser letzte Term ist eindeutig weniger wichtig als der zweite. Wenn wir aber weiter gehen und dx nur als $\frac{1}{1000}$ von x auffassen, dann ist der zweite Term $\frac{2}{1000}$ von x², während der dritte Term nur $\frac{1}{1.000.000}$ von x² ist.

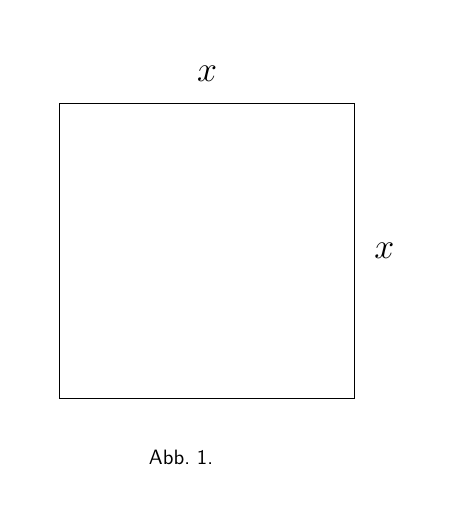
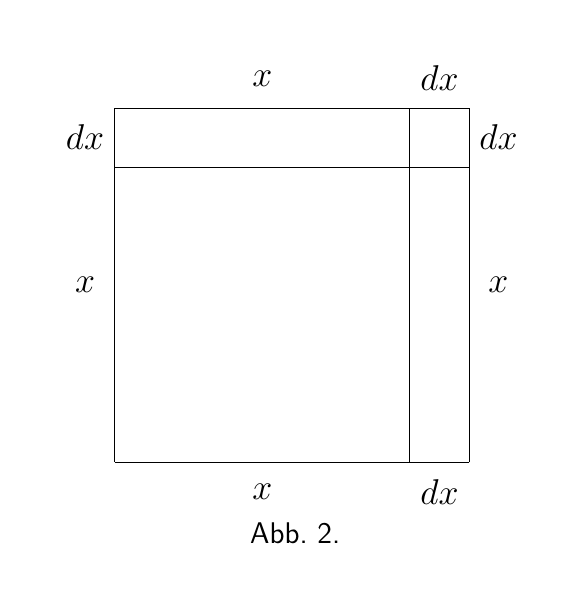
Geometrisch lässt sich dies wie folgt darstellen: Zeichnen Sie ein Quadrat (Abbildung 1), dessen Seite wir für x halten. Nehmen wir nun an, das Quadrat vergrößere sich, indem es in jeder Richtung um ein Stück dx vergrößert wird. Das vergrößerte Quadrat setzt sich zusammen aus dem ursprünglichen Quadrat x², den beiden Rechtecken oben und rechts, die jeweils den Flächeninhalt x · dx (oder zusammen 2x · dx) haben, und dem kleinen Quadrat in der rechten oberen Ecke, das (dx)² ist. In Abbildung 2 haben wir dx als einen ziemlich großen Bruchteil von x angenommen - etwa $\frac{1}{5}$. Aber nehmen wir an, wir hätten ihn nur als $\frac{1}{100}$ genommen - etwa die Dicke einer mit einem feinen Stift gezogenen Linie. Dann hätte das kleine Eckquadrat eine Fläche von nur $\frac{1}{10.000}$ von x² und wäre praktisch unsichtbar. Offensichtlich ist (dx)² vernachlässigbar, wenn wir nur die Schrittweite dx selbst als klein genug betrachten.

Lassen Sie uns ein Gleichnis betrachten.

Angenommen, ein Millionär würde zu seinem Sekretär sagen: Nächste Woche gebe ich dir einen kleinen Teil von jedem Geld, das bei mir eingeht. Nehmen wir an, der Sekretär würde zu seinem Jungen sagen: Ich werde dir einen kleinen Bruchteil von dem geben, was ich bekomme. Nehmen wir an, der Bruchteil sei in beiden Fällen jeweils $\frac{1}{100}$ der entsprechenden Summe. Wenn nun Herr Millionär in der nächsten Woche 10000 Euro erhält, würde der Sekretär 100 Euro und der Junge 1 Euro erhalten. Hundert Euro wären eine kleine Menge im Vergleich zu 10000 Euro; aber ein Euro ist in der Tat eine kleine Menge, von sehr untergeordneter Größe im Vergleich zu der ursprünglichen Summe von 10000 Euro. Aber um wie viel größer wäre das Missverhältnis, wenn der Bruchteil, statt $\frac{1}{100}$ zu sein, auf $\frac{1}{1000}$ Teil festgelegt worden wäre? Dann bekäme der Herr Millionär nach wie vor seine 10000 Euro, der Herr Sekretär aber nur noch 10 Euro, und der Junge 1 Cent!