Über das Bestimmen von Flächen durch Integrieren

Eine Anwendung der Integralrechnung ist es, die Werte von Flächen, die durch Kurven begrenzt sind, zu ermitteln.

Lassen Sie uns versuchen, dem Thema Stück für Stück näher zu kommen.

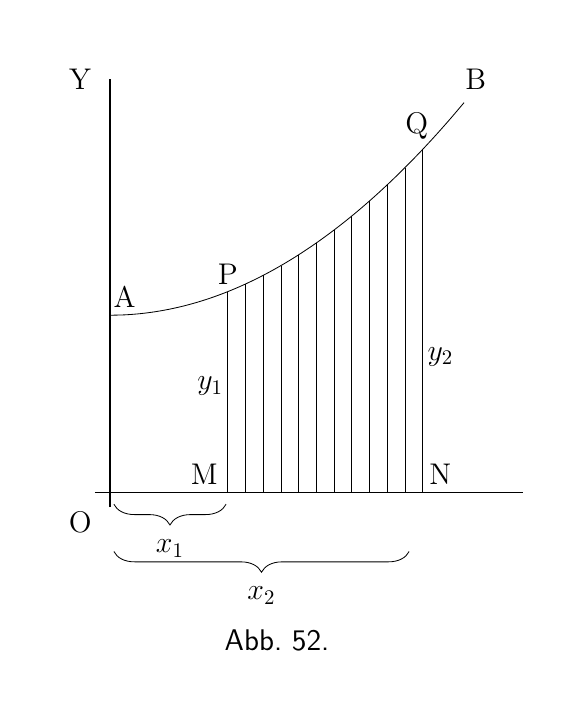
Lassen Sie AB (Abbildung 52) eine Kurve sein, deren Gleichung bekannt ist. Das heißt, y ist in dieser Kurve eine bekannte Funktion von x. Stellen Sie sich ein Stück der Kurve vom Punkt P zum Punkt Q vor.

Lassen Sie eine Senkrechte $PM$ vom Punkt P und eine weitere $QN$ vom Punkt Q fallen. Dann seien $OM = x_1$ und $ON = x_2$, und die Ordinaten $PM = y_1$ und $QN = y_2$. Damit haben wir die Fläche $PQNM$ abgesteckt, die unter dem Stück $PQ$ liegt. Das Problem ist, wie können wir den Wert dieser Fläche berechnen?

Das Geheimnis zur Lösung dieses Problems besteht darin, sich die Fläche als in viele schmale Streifen aufgeteilt vorzustellen, von denen jeder die Breite dx hat. Je kleiner wir dx nehmen, desto mehr davon gibt es zwischen $x_1$ und $x_2$. Nun ist die Gesamtfläche offensichtlich gleich der Summe der Flächen aller dieser Streifen. Unsere Aufgabe wird es nun sein, einen Ausdruck für die Fläche eines beliebigen schmalen Streifens zu finden und diesen zu integrieren, um alle Streifen zu addieren. Denken Sie nun an einen der Streifen. Er wird so aussehen: Er wird von zwei senkrechten Seiten begrenzt, hat eine flache Unterseite dx und eine leicht gekrümmte, schräge Oberseite.

Angenommen, wir nehmen ihre mittlere Höhe als y an; dann ist, da ihre Breite dx ist, ist ihre Fläche $y\, dx$. Und da wir die Breite so schmal nehmen können, wie wir wollen, wird, wenn wir sie nur schmal genug nehmen, ihre durchschnittliche Höhe gleich der Höhe in ihrer Mitte sein. Nennen wir nun den unbekannten Wert der gesamten Fläche $S$ (für Surface engl. Oberfläche bzw. Fläche), hier Fläche. Die Fläche eines Streifens wird einfach ein Teil der Gesamtfläche sein, und kann daher $dS$ genannt werden. Wir können also schreiben

\[ \text{Fläche eines 1-Streifens} = dS = y \cdot dx. \]

Wenn wir dann alle Streifen zusammenzählen, erhalten wir

\[ \text{Gesamtfläche $S$} = \int dS = \int y\, dx. \]

Dass wir $S$ finden, hängt also davon ab, ob wir $y \cdot dx$ für den speziellen Fall integrieren können, also wenn wir wissen, wie groß der Wert von y in Abhängigkeit von x ist. M.a.W. wenn wir die Funktion kennen.

Wenn Ihnen zum Beispiel gesagt würde, dass für die betreffende Kurve $y = b + ax^2$ gilt, könnten Sie zweifellos diesen Wert in den Ausdruck einsetzen und sagen: Dann muss ich $\int (b + ax^2)\, dx$ finden.

Das ist alles schön und gut; aber ein wenig Nachdenken wird Ihnen zeigen, dass etwas mehr getan werden muss. Da die Fläche, die wir zu finden versuchen, nicht die Fläche unter der gesamten Länge der Kurve ist, sondern nur die Fläche, die links durch $PM$ und rechts durch $QN$ begrenzt ist, daraus folgt, dass wir etwas tun müssen, um unsere Fläche zwischen diesen Grenzen zu definieren.

Dies führt uns zu einem neuen Begriff, nämlich dem des Integrierens zwischen Grenzen. Wir nehmen an, dass x variiert, und für den vorliegenden Fall benötigen wir weder einen Wert von x unterhalb von $x_1$ (also $OM$) noch einen Wert von x oberhalb von $x_2$ (also $ON$). Wenn ein Integral auf diese Weise zwischen zwei Grenzen definiert werden soll, nennen wir den unteren der beiden Werte die untere Grenze und den oberen Wert die obere Grenze. Ein so begrenztes Integral bezeichnen wir als bestimmtes Integral beziehungsweise als definites Integral, um es von einem unbestimmten Integral beziehungsweise allgemeinen Integral zu unterscheiden, dem keine Grenzen zugeordnet sind.

In den Symbolen, die Anweisungen zum Integrieren geben, werden die Grenzen markiert, indem man sie an den oberen beziehungsweise unteren Rand des Integrationszeichens setzt.
So steht die Anweisung

\[ \int_{x=x_1}^{x=x_2} y \cdot dx \]

dafür: Finde das Integral von $y \cdot dx$ zwischen der unteren Grenze $x_1$ und der oberen Grenze $x_2$.

Manchmal wird das Ganze auch einfacher geschrieben

\[ \int^{x_2}_{x_1} y \cdot dx. \]

Nun, aber wie findet man ein Integral zwischen Grenzwerten, wenn man diese Aufgabe hat?

Schauen Sie sich noch einmal Abbildung 52 an. Angenommen, wir könnten die Fläche unter dem größeren Kurvenstück von A bis Q, also von $x = 0$ bis $x = x_2$, finden und nennen die Fläche $AQNO$. Dann nehmen wir an, wir könnten die Fläche unter dem kleineren Kurvenstück von A bis P, also von $x = 0$ bis $x = x_1$, finden, nämlich die Fläche $APMO$. Wenn wir dann die kleinere Fläche von der größeren subtrahieren würden, müsste als Rest die Fläche $PQNM$ übrig bleiben, was wir ja wollen. Hier haben wir den Anhaltspunkt, was zu tun ist; das bestimmte Integral zwischen den beiden Grenzen ist die Differenz zwischen dem für die obere Grenze errechneten Integral und dem für die untere Grenze errechneten Integral.

Lassen Sie uns also fortfahren. Zunächst bestimmen wir das unbestimmte/allgemeine Integral:

\[ \int y\, dx, \]

Und da $y = b + ax^2$ die Gleichung für die Kurve (Abbildung 52) ist,

\[ \int (b + ax^2)\, dx \]

das unbestimmte/allgemeine Integral, das wir finden müssen.

Wenn wir die Integration nach den Regeln durchführen, erhalten wir

\[ bx + \frac{a}{3} x^3 + C; \]

Und dies ist die gesamte Fläche von 0 bis zu einem beliebigen Wert von x, den wir festlegen / einsetzen können.

Der größere Bereich bis zur oberen Grenze $x_2$ ist also

\[ bx_2 + \frac{a}{3} x_2^3 + C; \]

und die kleinere Fläche bis zur unteren Grenze $x_1$ ist dann

\[ bx_1 + \frac{a}{3} x_1^3 + C. \]

Ziehen wir nun die kleinere von der größeren Fläche ab, so erhalten wir für die Fläche $S$ den Wert,

\[ \text{Fläche $S$} = b(x_2 - x_1) + \frac{a}{3}(x_2^3 - x_1^3). \]

Das ist die Antwort, die wir wollten. Geben wir nun einige Zahlenwerte an. Nehmen wir an, dass $b = 10$, $a = 0,06$, sowie $x_2 = 8$ und $x_1 = 6$. Dann ist die Fläche $S$ gleich

\begin{gather*} 10(8 - 6) + \frac{0,06}{3} (8^3 - 6^3) \\ \begin{aligned} &= 20 + 0,02(512 - 216) \\ &= 20 + 0,02 \times 296 \\ &= 20 + 5,92 \\ &= 25,92. \end{aligned} \end{gather*}

Lassen Sie uns hier symbolisch festhalten, was wir über die Grenzen herausgefunden haben:

\[ \int^{x=x_2}_{x=x_1} y\, dx = y_2 - y_1, \]

Dabei ist $y_2$ der integrierte Wert von $y\, dx$ entsprechend $x_2$ und $y_1$ derjenige entsprechend $x_1$.

Bei jeder Integration zwischen Grenzen muss also die Differenz zwischen zwei Werten gefunden werden. Beachten Sie auch, dass bei der Subtraktion die addierte Konstante $C$ verschwunden ist.

Beispiele
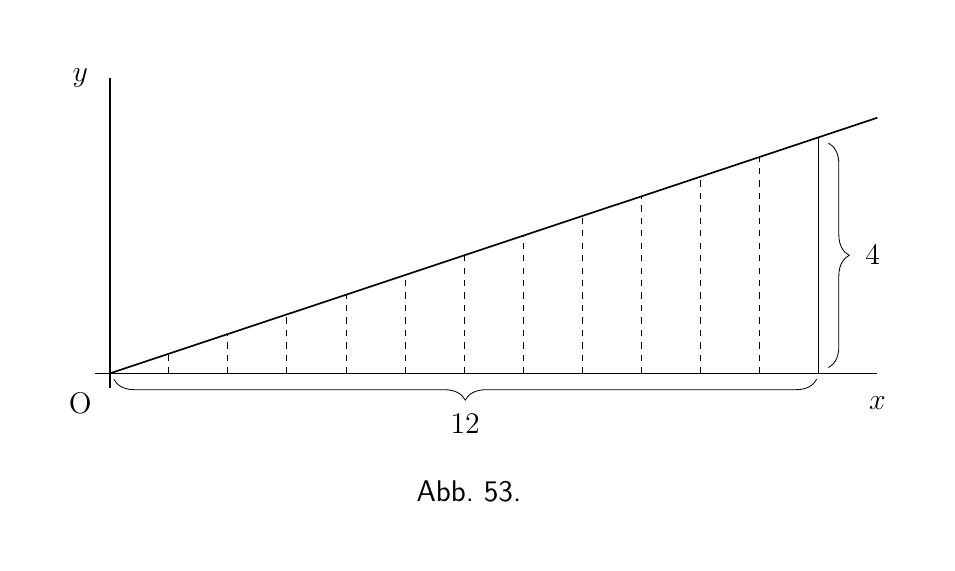
(1) Um uns mit dem Verfahren vertraut zu machen, nehmen wir einen Fall, von dem wir die Antwort schon vorher kennen. Wir wollen den Flächeninhalt des Dreiecks (Abbildung 53) bestimmen, das die Basis $x = 12$ und die Höhe $y = 4$ hat. Da wir die Abmessungen kennen, wissen wir bereits vorher schon, dass die Antwort 24 lauten wird.

Nun haben wir hier als Kurve eine schräge Linie, für die die Gleichung lautet

\[ y = \frac{x}{3}. \]

Die Fläche, um die es geht, ist

\[ \int^{x=12}_{x=0} y \cdot dx = \int^{x=12}_{x=0} \frac{x}{3} \cdot dx. \]

Integriert man $\dfrac{x}{3}\, dx$ (hier), und setzt den Wert des unbestimmte/allgemeinen Integrals in eckige Klammern, wobei die Grenzen oben und unten markiert sind, so erhält man

\begin{align*} \text{Fläche }\; &= \left[ \frac{1}{3} \cdot \frac{1}{2} x^2 \right]^{x=12}_{x=0} + C \\ &= \left[ \frac{x^2}{6} \right]^{x=12}_{x=0} + C \\ &= \left[ \frac{12^2}{6} \right] - \left[ \frac{0^2}{6} \right] \\\ &= \frac{144}{6} = 24.\quad \text{Antwort}. \end{align*}

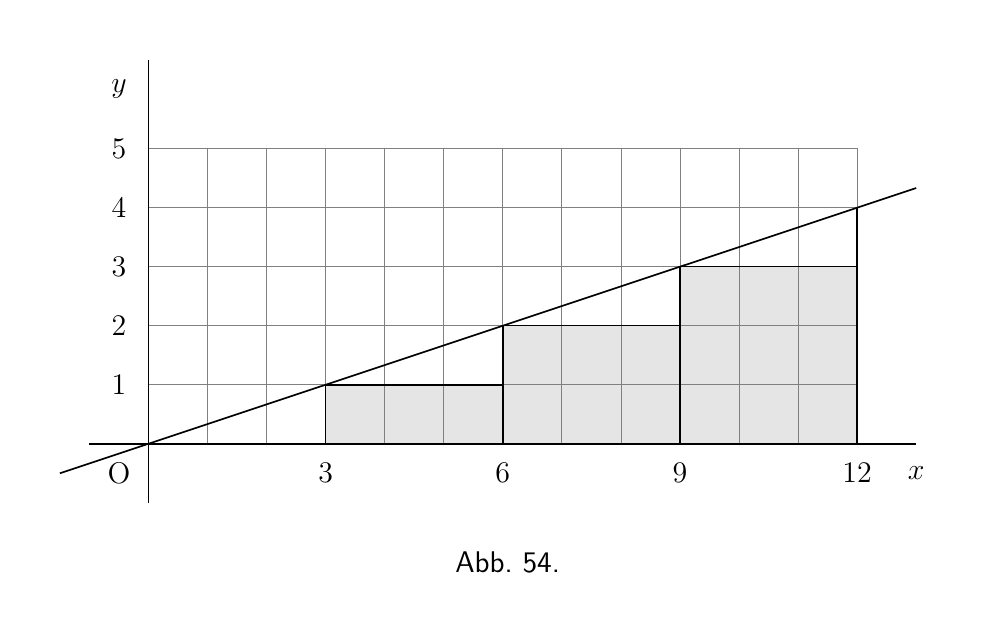
Überzeugen wir uns von diesem recht überraschenden Rechenweg, indem wir ihn an einem einfachen Beispiel ausprobieren. Besorgen Sie sich ein kariertes Papier, vorzugsweise eines, das in kleinen Quadraten von je einem halben Zentimeter liniert ist. Zeichnen Sie auf diesem Papier den Graphen der Gleichung,

\[ y = \frac{x}{3}. \]

Die zu zeichnenden Werte sind:

x	0	3	$6$	$9$	12
y	0	1	2	3	4

Die Darstellung findet sich in Abbildung 54.

Berechnen Sie nun die Fläche unter der Kurve durch Zählen der kleinen Quadrate unterhalb der Linie, von $x = 0$ bis $x = 12$. Es gibt $18$ ganze Quadrate und vier Dreiecke, von denen jedes eine Fläche hat, die $1\frac{1}{2}$ Quadraten entspricht; insgesamt also 24 Quadrate. Daher ist 24 der numerische Wert des Integrals von $\dfrac{x}{3}\, dx$ zwischen der unteren Grenze von $x = 0$ und der oberen Grenze von $x = 12$.

Zeigen Sie, als weitere Übung, dass der Wert des gleichen Integrals zwischen den Grenzen $x = 3$ und $x = 15$ den (numerischen) Wert 36 besitzt.

(2) Bestimmen Sie die Fläche unter der Kurve $y = \dfrac{b}{x + a}$ zwischen den Grenzen $x = x_1$ und $x = 0$.

\begin{align*} \text{Fläche} &= \int^{x=x_1}_{x=0} y \cdot dx = \int^{x=x_1}_{x=0} \frac{b}{x+a}\, dx \\ &= b \bigl[\log_\epsilon(x + a) \bigr]^{x_1} _{0} + C \\ &= b \bigl[\log_\epsilon(x_1 + a) - \log_\epsilon(0 + a)\bigr] \\ &= b \log_\epsilon \frac{x_1 + a}{a}.\quad Antwort . \end{align*}

Hinweis Beachten Sie, dass beim Umgang mit bestimmten/definitiven Integralen die Konstante $C$ immer durch Subtraktion verschwindet.

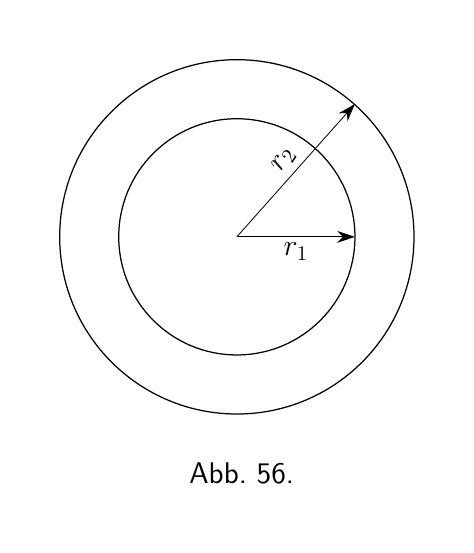
An dieser Stelle sei angemerkt, dass dieses Verfahren, einen Teil von einem größeren zu subtrahieren, um die Differenz zu finden, durchaus gängige Praxis ist. Wie bestimmt man den Flächeninhalt eines ebenen Rings (Abbildung 56), dessen äußerer Radius $r_2$ und der innere Radius $r_1$ ist? Man weiß aus der Formelsammlung (Fläche eines Kreises), dass der Flächeninhalt des äußeren Kreises $\pi r_2^2$ ist; dann bestimmt man den Flächeninhalt des inneren Kreises, $\pi r_1^2$; dann subtrahiert man Letzteren vom Ersteren und findet so, den Flächeninhalt des Rings $= \pi(r_2^2 - r_1^2)$; das kann man schreiben als

\[ \pi(r_2 + r_1)(r_2 - r_1) \] $= \text{Mittelwert des Ringumfangs} \times \text{Breite des Rings}$.

Der Mittelwert des Ringumfangs lässt sich durch die Umfänge des äußeren und inneren Kreises berechnen, und ist $\dfrac{2\pi \cdot r_2 + 2\pi \cdot r_1}{2} = \pi \cdot r_2 + \pi \cdot r_1 = \pi (r_2 + r_1)$. Die Breite des Rings ergibt sich aus der Differenz der Radi des äußeren und inneren Kreises, also $r_2 - r_1$.

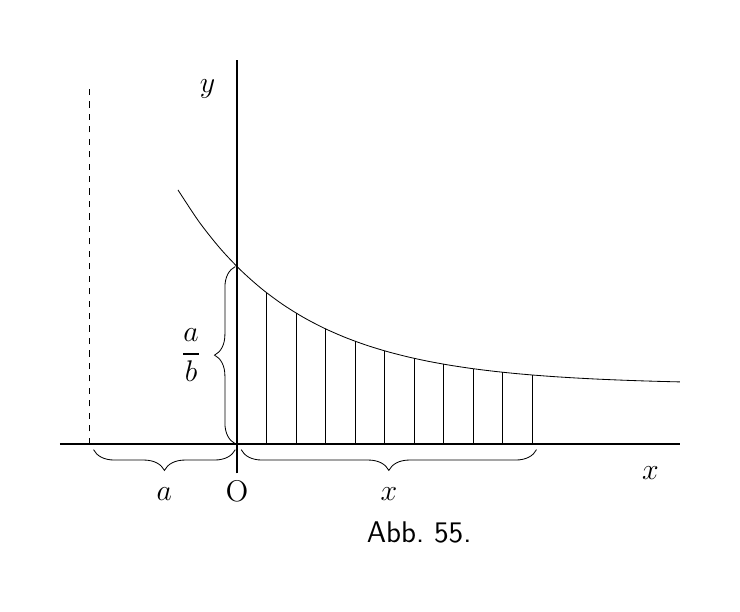
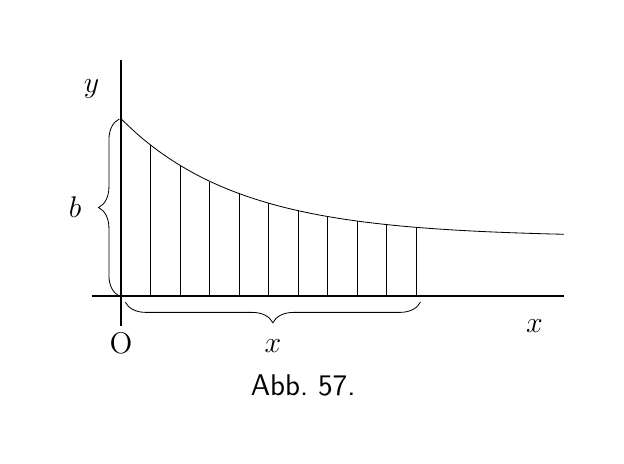
(3) Hier ist ein weiterer Fall, der der Zerfallskurve. Bestimmen Sie die Fläche, zwischen $x = 0$ und $x = a$, der Kurve (Abbildung 57), deren Gleichung

\begin{align*} y &= b\epsilon^{-x}. \\ \text{Fläche } &= b\int^{x=a} _{x=0} \epsilon^{-x} \cdot dx \\ \end{align*}

lautet.

Die Integration (hier) ergibt

\begin{align*} &= b\left[-\epsilon^{-x}\right]^a _0 \\ &= b\bigl[-\epsilon^{-a} - (-\epsilon^{-0})\bigr] \\\ &= b(1-\epsilon^{-a}). \end{align*}

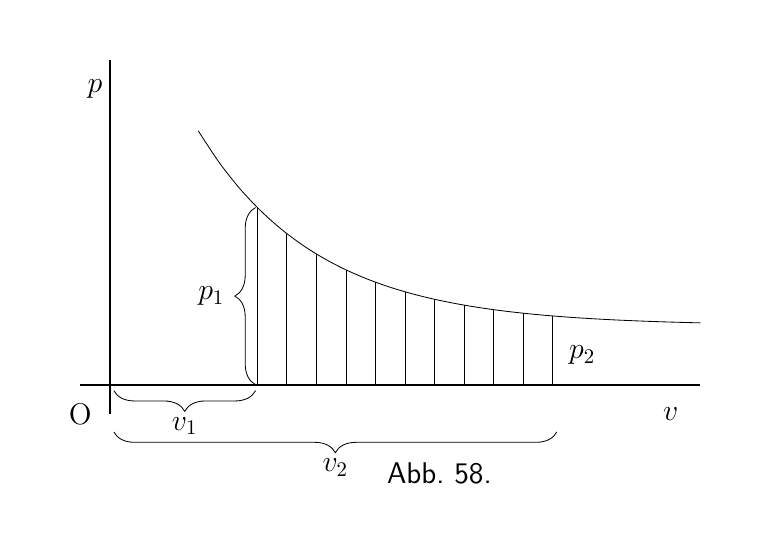
(4) Ein weiteres Beispiel bietet die adiabatische Kurve eines perfekten Gases, deren Gleichung $pv^n = c$ lautet, wobei $p$ für den Druck, v für das Volumen und n den Wert $1,42$ hat (Abbildung 58).

Bestimmen Sie die Fläche unter der Kurve (die proportional zur Arbeit ist, die bei der plötzlichen Kompression des Gases geleistet wird) vom Volumen $v_2$ zum Volumen $v_1$.

Hier haben wir \begin{align*} \text{Fläche } &= \int^{v=v_2}_{v=v_1} cv^{-n} \cdot dv \\ &= c\left[\frac{1}{1-n} v^{1-n} \right]^{v_2} _{v_1} \\ &= c \frac{1}{1-n} (v_2^{1-n} - v_1^{1-n}) \\ &= \frac{-c}{0.42}\left(\frac{1}{v_2^{0.42}} - \frac{1}{v_1^{0.42}}\right). \end{align*}

Eine Übung.

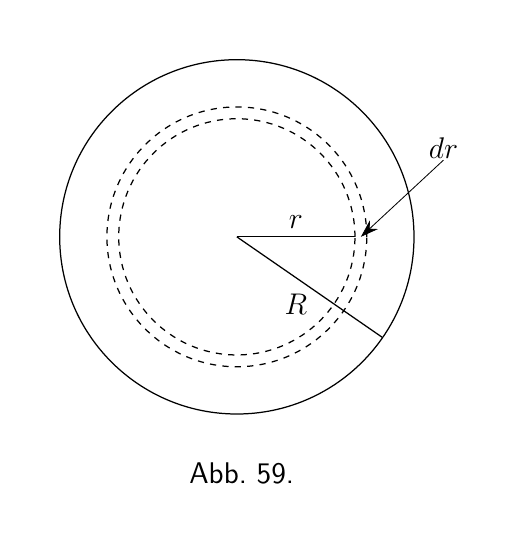
Beweise Sie, dass die Formel die gewöhnlich für die Berechnung der Fläche A eines Kreises, dessen Radius $R$ ist, verwendet wird, gleich $\pi R^2$ ist.

Betrachten wir eine Elementarzone beziehungsweise einen Ring der Fläche (Abbildung 59), mit der Breite $dr$, die sich in einem Abstand r vom Zentrum befindet. Wir können die gesamte Oberfläche, als aus solchen schmalen Zonen bestehend betrachten, und die gesamte Fläche A wird einfach das Integral aller solcher elementaren Zonen von der Mitte bis zum Rand sein, integriert von $r = 0$ bis $r = R$.

Wir müssen also einen Ausdruck für die Elementarfläche $dA$ der schmalen Zone finden. Stellen Sie sich diese als einen Streifen der Breite $dr$ und einer Länge vor, die dem Umfang des Kreises mit dem Radius r entspricht, also einer Länge von $2 \pi r$. Dann haben wir als Fläche der schmalen Zone,

\[ dA = 2 \pi r\, dr. \]

Der Flächeninhalt des gesamten Kreises ist demnach:

\[ A = \int dA = \int^{r=R}_{r=0} 2 \pi r \cdot dr = 2 \pi \int^{r=R}_{r=0} r \cdot dr. \]

Nun ist das unbestimmte/allgemeine Integral von $r \cdot dr$ ist $\frac{1}{2} r^2$. Daraus folgt:

\begin{align*} A &= 2 \pi \bigl[\tfrac{1}{2} r^2 \bigr]^{r=R}_{r=0}; \\ \text{ } A &= 2 \pi \bigl[\tfrac{1}{2} R^2 - \tfrac{1}{2}(0)^2\bigr]; \\ \text{und daher } \; A &= \pi R^2. \end{align*}

Eine weitere Übung

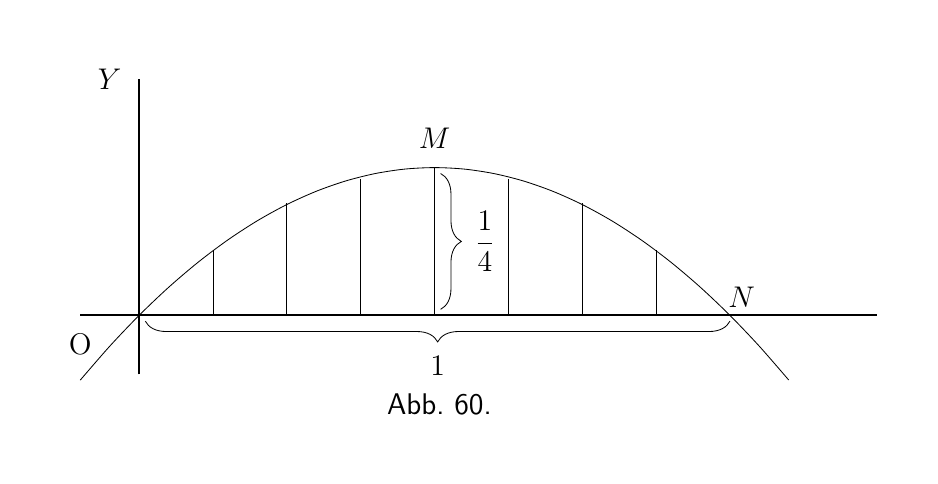
Wir bestimmen die mittlere Ordinate, des positiven Teils, der Kurve $y = x - x^2$, die in Abbildung 60 dargestellt ist. Um die mittlere Ordinate zu finden, müssen wir den Flächeninhalt des Stücks $OMN$ bestimmen und diesen dann durch die Länge der Basis $ON$ teilen. Bevor wir aber den Flächeninhalt bestimmen können, müssen wir die Länge der Basis ermitteln, um zu wissen, bis zu welcher Grenze wir integrieren sollen. Bei $N$ hat die Ordinate y den Wert null; wir müssen also die Gleichung betrachten und sehen, bei welchem Wert von x $y = 0$ wird. Nun ist klar, wenn x 0 ist, dann wird y auch 0 sein, da die Kurve geht durch den Ursprung $O$; es gilt aber auch, dass wenn $x=1$ ist, dann ist $y=0$; so dass $x=1$ uns die Position des Punktes $N$ gibt.

Die gesuchte Fläche ist dann \begin{align*} &= \int^{x=1}_{x=0} (x-x^2)\, dx \\ &= \left[\tfrac{1}{2} x^2 - \tfrac{1}{3} x^3 \right]^{1}_{0} \\ &= \left[\tfrac{1}{2} - \tfrac{1}{3} \right] - [0-0] \\ &= \tfrac{1}{6}. \end{align*}

Da die Basislänge 1 ist. Ist die mittlere Ordinate der Kurve $= \frac{1}{6}$.

Anmerkung: Es ist eine schöne und einfache Übung in Maxima und Minima, durch Differenzieren herauszufinden, wie hoch die maximale Ordinate ist. Sie muss größer sein als der Mittelwert.

Die mittlere Ordinate einer beliebigen Kurve, über einen Bereich von $x= 0$ bis $x = x_1$, ist durch den Ausdruck,

\[ \text{mittleres y} = \frac{1}{x_1} \int^{x=x_1}_{x=0} y \cdot dx \]

gegeben.

Auf die gleiche Weise kann man auch den Flächeninhalt eines Rotationskörpers ermitteln.

Beispiel

Die Kurve $y=x^2 - 5$ dreht sich um die Achse von x. Bestimmen Sie den Flächeninhalt, der von der Kurve erzeugten Fläche, zwischen $x=0$ und $x=6$.

Ein Punkt auf der Kurve, deren Ordinate y ist, beschreibt einen Umfang der Länge $2\pi y$, und ein schmaler Streifen der Fläche mit der Breite dx, der zu diesem Punkt gehört, hat für den Flächeninhalt $2\pi y dx$. Die Gesamtfläche ist

\begin{align*} 2\pi \int^{x=6}_{x=0} y\, dx &= 2\pi \int^{x=6}_{x=0} (x^2-5)\, dx\\ &= 2\pi \left[\frac{x^3}{3} - 5x\right]^6_0 \\ &= 6,28 \times 42\\ & =263,76. \end{align*}