Über quadratische Mittelwerte

In bestimmten Bereichen der Physik, insbesondere bei der Untersuchung elektrischer Wechselströme, ist es notwendig, das quadratische Mittel einer variablen Größe berechnen zu können. Mit quadratischem Mittelwert bezeichnet man die Quadratwurzel aus dem Mittelwert der Quadrate aller Werte zwischen den betrachteten Grenzen. Andere Bezeichnungen für den quadratischen Mittelwert einer beliebigen Größe sind sein virtueller Wert oder sein r.m.s. (d.h. root-mean-square) Wert. Der französische Begriff ist valeur efficace . Wenn y die betrachtete Funktion ist und der quadratische Mittelwert zwischen den Grenzen von $x=0$ und $x=l$ genommen werden soll; dann wird der quadratische Mittelwert ausgedrückt als

\[ \sqrt[2] {\frac{1}{l} \int^l_0 y^2\, dx}. \]

Beispiele

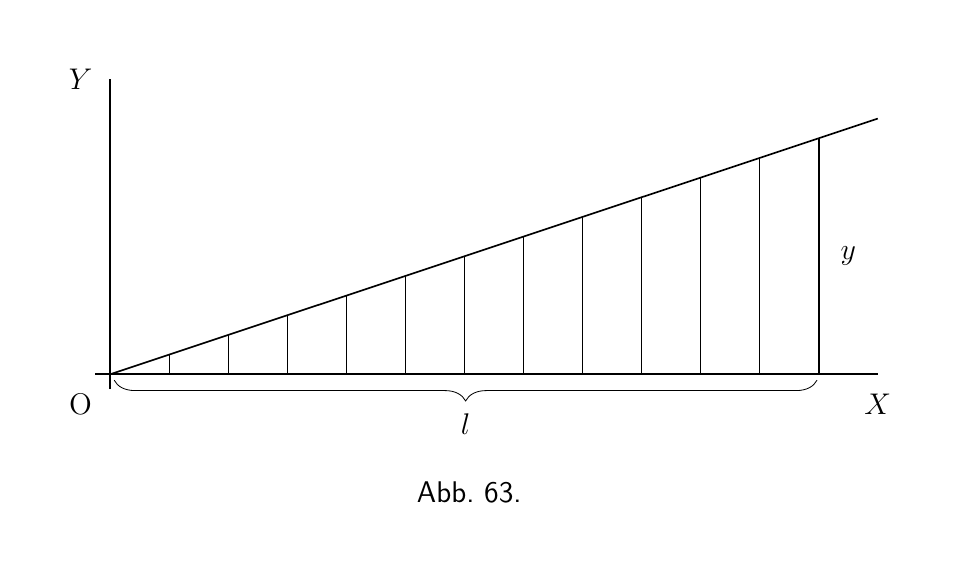
(1) Es soll das quadratische Mittel der Funktion $y=ax$ (Abbildung 63) gefunden werden.

Hier ist das Integral $\int^l_0 a^2 x^2\, dx$, das ist $\frac{1}{3} a^2 l^3$.

Teilt man durch l und zieht die Quadratwurzel, so erhält man:

\[ \text{quadratisches Mittel} = \frac{1}{\sqrt 3}\, al. \]

Hier ist das arithmetische Mittel $\frac{1}{2}al$; und das Verhältnis von quadratischem zu arithmetischem Mittel (dieses Verhältnis nennt man den Formfaktor) ist $\dfrac{2}{\sqrt 3}=1,155$.

(2) Es soll das quadratische Mittel der Funktion $y=x^a$ gefunden werden.

Das Integral ist $\int^{x=l}_{x=0} x^{2a}\, dx$, also $\dfrac{l^{2a+1}}{2a+1}$.

Daraus folgt: quadratisches Mittel = $\sqrt[2]{\dfrac{l^{2a}}{2a+1}}$.

(3) Es soll das quadratische Mittel der Funktion $y=a^{\frac{x}{2}}$ bestimmt werden.

Das Integral ist $\int^{x=l}_{x=0} (a^{\frac{x}{2}})^2\, dx$, also $\int^{x=l}_{x=0} a^x\, dx$,

$\left[ \frac{a^x}{\log_\epsilon a} \right]^{x=l}_{x=0}$, was $\dfrac{a^l-1}{\log_\epsilon a}$ ist.

Das quadratische Mittel ist also $\sqrt[2] {\dfrac{a^l - 1}{l \log_\epsilon a}}$.

Übungen XVIII

(1) Bestimmen Sie den Flächeninhalt der Kurve $y=x^2+x-5$ zwischen $x=0$ und $x=6$ sowie die mittleren Ordinaten zwischen diesen Grenzen.

(2) Bestimmen Sie den Flächeninhalt der Parabel $y=2a\sqrt x$ zwischen $x=0$ und $x=a$. Zeigen Sie, dass er zwei Drittel des Rechtecks der begrenzenden Ordinate und ihrer Abszisse beträgt.

(3) Bestimmen Sie den Flächeninhalt des positiven Teils einer Sinuskurve und der mittleren Ordinate.

(4) Bestimmen Sie den Flächeninhalt des positiven Anteils der Kurve $y=\sin^2 x$ und die mittlere Ordinate.

(5) Bestimmen Sie die Fläche, die zwischen den beiden Schenkeln der Kurve $y=x^2 ? x^{\frac{5}{2}}$ von $x=0$ bis $x=1$ eingeschlossen ist, und außerdem die Fläche des positiven Anteils des unteren Schenkels der Kurve (siehe Abbildung 30).

(6) Bestimmen Sie das Volumen eines Kegels mit dem Radius der Grundfläche r und der Höhe h.

(7) Bestimmen Sie den Flächeninhalt der Kurve $y=x^3-\log_\epsilon x$ zwischen $x=0$ und $x=1$.

(8) Bestimmen Sie das Volumen, das die Kurve $y=\sqrt{1+x^2}$ bei ihrer Drehung um die Achse x zwischen $x=0$ und $x=4$ erzeugt.

(9) Bestimmen Sie das Volumen, das eine Sinuskurve erzeugt, die um die Achse von x kreist. Finde auch den Flächeninhalt ihrer Oberfläche.

(10) Bestimmen Sie den Flächeninhalt des Teils der Kurve $xy=a$, der zwischen $x=1$ und $x = a$ liegt. Bestimmen Sie die mittlere Ordinate zwischen diesen Grenzen.

(11) Zeigen Sie, dass das quadratische Mittel der Funktion $y=\sin x$ zwischen den Grenzen 0 und $\pi$ im Bogenmaß $\dfrac{\sqrt2}{2}$ ist. Bestimmen Sie auch das arithmetische Mittel derselben Funktion zwischen denselben Grenzen; und zeigen Sie, dass der Formfaktor $=1,11$ ist.

(12) Bestimmen Sie das arithmetische und das quadratische Mittel der Funktion $x^2+3x+2$, von $x=0$ bis $x=3$.

(13) Bestimmen Sie den quadratischen und den arithmetischen Mittelwert der Funktion $y=A_1 \sin x + A_1 \sin 3x$.

(14) Eine bestimmte Kurve hat die Gleichung $y=3,42\epsilon^{0,21x}$. Bestimmen Sie die Fläche, die zwischen der Kurve und der Achse von x eingeschlossen ist, von der Ordinate bei $x=2$ bis zur Ordinate bei $x = 8$. Bestimmen Sie auch die Höhe der mittleren Ordinate der Kurve zwischen diesen Punkten.

(15) Bestimmen Sie das Volumen, das von der Kurve $y=\pm \dfrac{x}{6}\sqrt{x(10-x)}$ erzeugt wird, die sich um die Achse von x dreht.

Antworten

(1) $\text{Fläche} = 60$; $\text{Mittelwert Ordinate} = 10$.

(2) $\text{Fläche} = \frac{2}{3}$ von $a \times 2a \sqrt{a}$.

(3) $\text{Fläche} = 2$; $\text{Mittelwert Ordinate} = \dfrac{2}{\pi} = 0,637$.

(4) $\text{Fläche} = 1,57$; $\text{mittlere Ordinate} = 0,5$.

(5) $0,572$; $0,0476$.

(6) $\text{Volumen} = \pi r^2 \dfrac{h}{3}$.

(7) $1,25$.

(8) $79,4$.

(9) $\text{Volumen} = 4,9348$; $\text{Flächeninhalt} = 12,57$ (von 0 bis $\pi$).

(10) $a\log_\epsilon a$, ? ? $\dfrac{a}{a - 1} \log_\epsilon a$.

(12) $\text{Arithmetisches Mittel} = 9,5$; $\text{quadratisches Mittel} = 10,85$.

(13) $\text{Quadratisches Mittel} = \dfrac{1}{\sqrt{2}} \sqrt{A_1^2 + A_3^2}$; $\text{arithmetisches Mittel} = 0$.

Das erste beinhaltet ein schwieriges Integral und kann so formuliert werden: Per Definition ist das quadratische Mittel:

\[ \sqrt{\dfrac{1}{2\pi} \int_0^{2\pi} (A_1 \sin x + A_3 \sin 3x)^2\, dx}. \]

Die durch

\[ \int (A_1^2 \sin^2 x + 2A_1 A_3 \sin x \sin 3x + A_3^2 \sin^2 3x)\, dx \]

vorgegebene Integration ist leichter, zu erhalten, wenn wir für $\sin^2 x$ schreiben

\[ \dfrac{1 - \cos 2x}{2}. \]

Für $2\sin x \sin 3x$ schreiben wir $\cos 2x - \cos 4x$; und, für $\sin^2 3x$,

\[ \dfrac{1 - \cos 6x}{2}. \]

Nachdem wir diese Substitutionen vorgenommen und integriert haben, erhalten wir (siehe hier)

\[ \dfrac{A_1^2}{2} \left( x - \dfrac{\sin 2x}{2} \right) + A_1 A_3 \left( \dfrac{\sin 2x}{2} - \dfrac{\sin 4x}{4} \right) + \dfrac{A_3^2}{2} \left( x - \dfrac{\sin 6x}{6} \right). \]

An der unteren Grenze lässt die Ersetzung von 0 für x all dies verschwinden, während an der oberen Grenze die Ersetzung von $2\pi$ für x $A_1^2 \pi + A_3^2 \pi$ ergibt. Und daraus folgt die Antwort.

(14) Der Flächeninhalt beträgt $62,6$ Quadrateinheiten. Die mittlere Ordinate ist $10,42$.

(15) $436,3$. (Dieser Körper ist birnenförmig.)