Krümmung der Kurven
Um auf den Prozess der nacheinander stattfindenden Differenzierung zurückzukommen, kann man fragen: Warum will jemand zweimal differenzieren? Wir wissen, dass, wenn die veränderlichen Größen Raum und Zeit sind, wir durch zweimaliges Differenzieren die Beschleunigung eines bewegten Körpers erhalten, und dass in der geometrischen Interpretation, angewendet auf Kurven, $\dfrac{dy}{dx}$ die Steigung der Kurve bedeutet. Aber was kann $\dfrac{d^2 y}{dx^2}$ in diesem Fall bedeuten? Es bedeutet eindeutig die Rate (pro Längeneinheit x), mit der sich die Steigung ändert, kurz gesagt, es ist ein Maß für die Krümmung der Steigung.
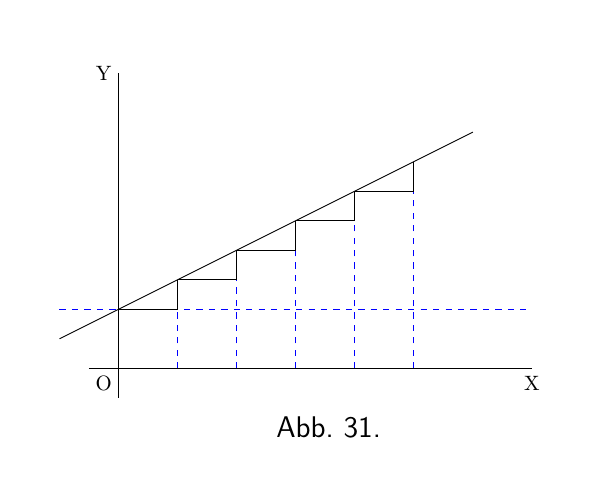
Angenommen die Steigung ist konstant wie in Abbildung 31.
Dann besitzt $\dfrac{dy}{dx}$ einen konstanten Wert.
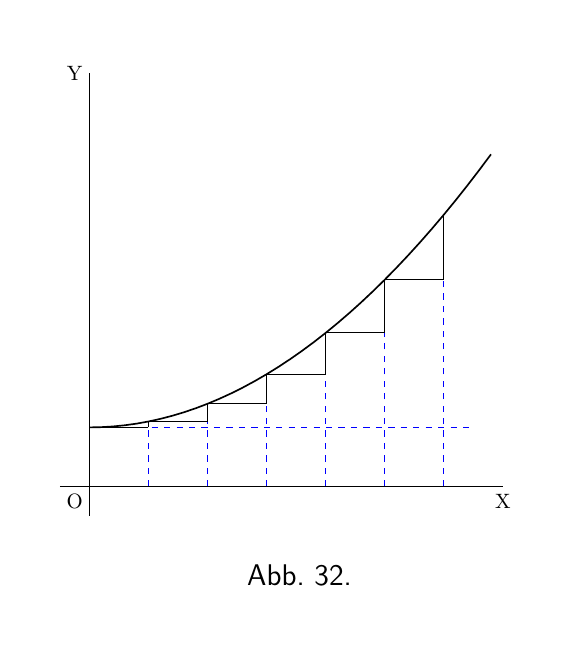
Nehmen wir jedoch einen Fall an, in dem, wie in Abbildung 32, die Steigung selbst nach oben größer wird, dann $\dfrac{d\left(\dfrac{dy }{dx}\right)}{dx}$, d. h. $\dfrac{d^2y}{dx^2}$, wird positiv sein.
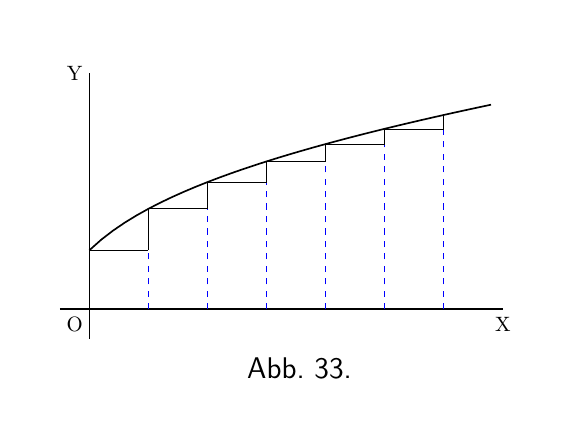
Wenn die Steigung nach rechts abnimmt wie in Abbildung 14 oder wie in Abbildung 33: Obwohl die Kurve nach oben geht, ist ihr $ \dfrac{d^2y}{dx^2} $ negativ, da die Änderung die Steigung sich verringert.
?
Jetzt ist es an der Zeit, Sie in ein weiteres Geheimnis einzuweihen - wie Sie feststellen können, ob das Ergebnis, das Sie durch "gleich Null setzen" erhalten, ein Maximum oder ein Minimum ist. Der Trick ist folgender: Nachdem Sie differenziert haben (um den Ausdruck zu erhalten, den Sie mit null gleichsetzen), differenzieren Sie ein zweites Mal und prüfen, ob das Ergebnis der zweiten Differenzierung positiv oder negativ ist. Wenn $ \dfrac{d^2y}{dx^2}$ positiv ist, wissen Sie, dass der Wert von y, den Sie erhalten haben, ein Minimum war; aber wenn $\dfrac{d^2y}{dx^2}$ negativ herauskommt, dann muss der Wert von y, den Sie erhalten, ein Maximum sein. Das ist die Regel.
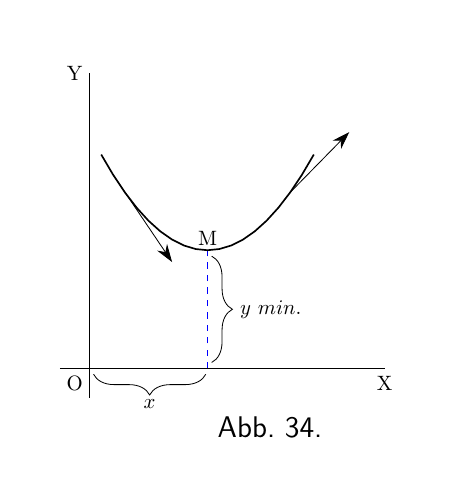
Der Grund dafür sollte ziemlich offensichtlich sein. Stellen Sie sich eine Kurve mit einem Minimum Punkt vor wie in Abbildung 15 oder wie Abbildung 34, wobei der Punkt des Minimums y mit $M$ markiert ist und die Kurve konkav nach oben verläuft. Links von $M$ geht die Steigung nach unten, d.h. negativ, und wird weniger negativ. Rechts von $M$ geht die Steigung nach oben und geht immer weiter nach oben. Offensichtlich ist die Änderung der Steigung, wenn die Kurve durch $M$ verläuft, sodass $\dfrac{d^2y}{dx^2}$ für seine Operation positiv ist, wenn x in Richtung rechts ansteigt, es wandelt eine Abwärtsneigung in eine Aufwärtsneigung um.
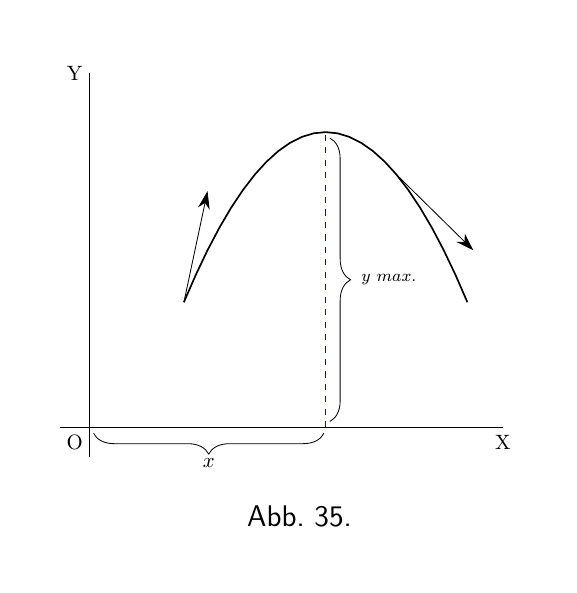
Betrachten Sie in ähnlicher Weise jede Kurve mit einem Maximum Punkt (wie Abbildung 16) oder wie Abbildung 35, wobei die Kurve konvex ist und der maximale Punkt mit $M$ markiert ist. Wenn die Kurve in diesem Fall $M$ von links nach rechts durchläuft, wird ihre Steigung in eine fallende oder negative Steigung umgewandelt, so dass in diesem Fall die Steigung der Steigung $\dfrac{ d^2y}{dx^2}$ ist negativ.
Kehren Sie nun zu den Beispielen des letzten Kapitels zurück und überprüfen Sie auf diese Weise die Schlussfolgerungen, ob es im Einzelfall ein Maximum oder ein Minimum gibt. Nachfolgend finden Sie einige ausgearbeitete Beispiele.
(1) Bestimmen Sie das Maximum oder Minimum von
\begin{align*} \text{(a)}\quad y &= 4x^2-9x-6; \qquad \text{(b)}\quad y = 6 + 9x-4x^2; \\ \end{align*}
und stellen Sie in allen Fällen fest, ob es sich jeweils um ein Maximum oder ein Minimum handelt.
\begin{align*} \text{(a)}\quad \dfrac{dy}{dx} &= 8x-9=0;\quad x=1\tfrac{1}{8},\quad \text{und } y = -11,065.\\ \dfrac{d^2y}{dx^2} &= 8;\quad \text{es ist $+$; (positv) und daher ein Minimum.} \\ \text{(b)}\quad {\dfrac{dy}{dx}} &= 9-8x=0;\quad x = 1\tfrac{1}{8};\quad \text{und } y = +11,065.\\ \dfrac{d^2y}{dx^2} &= -8;\quad \text{es ist $-$; (negativ) und daher ein Maximum.} \end{align*}
(2) Bestimmen Sie das Maxima oder Minima der Funktion
$y = x^3-3x+16$. \begin{align*} \dfrac{dy}{dx} &= 3x^2 - 3 = 0;\quad x^2 = 1;\quad \text{und } x = ?1.\\ \dfrac{d^2y}{dx^2} &= 6x;\quad \text{für $x = 1$; ist es $+$}; \end{align*}
Daher korrespondiert $x=1$ mit einem Minimum von $y=14$. Für $x=-1$ ist es $-$; und daher korrespondiert $x=-1$ mit einem Maximum von $y=+18$.
(3) Bestimmen Sie Maxima und Minima von $y=\dfrac{x-1}{x^2+2}$.
\[ \frac{dy}{dx} = \frac{(x^2+2) \times 1 - (x-1) \times 2x}{(x^2+2)^2} = \frac{2x - x^2 + 2}{(x^2 + 2)^2} = 0; \]
Bzw. $x^2 - 2x - 2 = 0$, wovon die Lösungen $x =+2,73$ und $x=-0,73$ sind.
\begin{align*} \dfrac{d^2y}{dx^2} &= - \frac{(x^2 + 2)^2 \times (2x-2) - (x^2 - 2x - 2)(4x^3 + 8x)}{(x^2 + 2)^4} \\ &= - \frac{2x^5 - 6x^4 - 8x^3 - 8x^2 - 24x + 8}{(x^2 + 2)^4}. \end{align*}
Der Nenner ist immer positiv, es reicht also, das Vorzeichen des Zählers zu ermitteln.
Wenn wir $x = 2,73$ einsetzen, wird der Zähler negativ; das Maximum, $y = 0,183$.
Wenn wir $x=-0,73$ einsetzen, wird der Zähler positiv; das Minimum, $y=-0,683$.
(4) Der Aufwand $C$ für den Umschlag der Produkte einer bestimmten Fabrik variiert mit der Wochenleistung P gemäß der Beziehung $C = aP + \dfrac{b}{c+P} + d$, wobei a, b, c, d positive Konstanten sind. Für welchen Output ist der Aufwand am geringsten?
\[ \dfrac{dC}{dP} = a - \frac{b}{(c+P)^2} = 0\quad \text{für Maximum oder Minimum;} \] $a = \dfrac{b}{(c+P)^2}$ und $P = \pm \sqrt{\dfrac{b}{a}} - c$.
Da der Output nicht negativ seien kann, $P=+\sqrt{\dfrac{b}{a}} - c$.
\begin{align*} \frac{d^2C}{dP^2} &= + \frac{b(2c + 2P)}{(c + P)^4}, \end{align*}
was für alle Werte von P positiv ist; daher entspricht, $P = +\sqrt{\dfrac{b}{a}} - c$ einem Minimum.
(5) Die Gesamtkosten pro Stunde $C$ für die Beleuchtung eines Gebäudes mit $N$ Lampen einer bestimmten Art betragen:
\[ C = N\left(\frac{C_l}{t} + \frac{EPC_e}{1000}\right), \] Wobei E die kommerzielle Effizienz (Watt pro Candela) ist. $ P $ ist die Lichtstärke (Candela) jeder Lampe, t ist die durchschnittliche Lebensdauer jeder Lampe in Stunden und $C_l =$ Erneuerungskosten in Pence pro Nutzungsstunde,$C_e =$ Energiekosten pro $1000$ Watt pro Stunde (kWh).
Außerdem beträgt die Beziehung zwischen der durchschnittlichen Lebensdauer einer Lampe und der kommerziellen Effizienz, mit der sie betrieben wird, ungefähr $t = mE^n$, wobei $m$ und n Konstanten in Abhängigkeit von der Art der Lampe sind.
Finden Sie die wirtschaftliche Effizienz, bei der die Gesamtkosten der Beleuchtung am geringsten sind.
\begin{align*} \text{ Wir haben }\; C &= N\left(\frac{C_l}{m} E^{-n} + \frac{PC_e}{1000} E\right), \\ \dfrac{dC}{dE} &= \frac{PC_e}{1000} - \frac{nC_l}{m} E^{-(n+1)} = 0 \end{align*}
für Maximum oder Minimum.
\[ E^{n+1} = \frac{1000 \times nC_l}{mPC_e}\quad \text{und}\quad E = \sqrt[n+1]{\frac{1000 \times nC_l}{mPC_e}}. \]
Dies ist eindeutig für das Minimum, da
\[ \frac{d^2C}{dE^2} = (n + 1) \frac{nC_l}{m} E^{-(n+2)}, \]
das ist positiv für einen positiven Wert von E.
Für einen bestimmten Typ von Lampen mit einer Lichtstärke (Kerzenleistung) von $16$ Candela wurden folgende Werte gefunden, $C_l= 17$ Pence, $C_e=5$ Pence, $ m = 10 $ und $ n = 3,6 $.
\[ E = \sqrt[4.6]{\frac{1000 \times 3.6 \times 17}{10 \times 16 \times 5}} = 2.6\text{Watt pro Kerzenleistung}. \]
Übungen X
(1) Bestimmen Sie Maxima und Minima von
\[ y = x^3 + x^2 - 10x + 8. \]
(2) Wenn $ y = \dfrac{b}{a} x - cx ^ 2 $ gegeben ist, bestimmen Sie die Ausdrücke für $ \dfrac{dy}{dx}$ und für $ \dfrac{d^2y}{dx^2}$. Bestimmen Sie auch den Wert von x, der y zu einem Maximum oder Minimum macht, und zeigen Sie, ob es ein Maximum oder ein Minimum ist.
(3) Finden Sie heraus, wie viele Maxima und wie viele Minima es in der Kurve gibt, deren Gleichung:
\[ y = 1 - \frac{x^2}{2} + \frac{x^4}{24}; \]
lautet und wie viele (Maxima/Minima) die Gleichung:
\[ y = 1 - \frac{x^2}{2} + \frac{x^4}{24} - \frac{x^6}{720} \text{ hat.} \]
(4) Bestimmen Sie Maxima und Minima von
\[ y=2x+1+\frac{5}{x^2}. \]
(5) Bestimmen Sie Maxima und Minima von
\[ y=\frac{3}{x^2+x+1}. \]
(6) Bestimmen Sie Maxima und Minima von
\[ y=\frac{5x}{2+x^2}. \]
(7) Bestimmen Sie Maxima und Minima von
\[ y=\frac{3x}{x^2-3} + \frac{x}{2} + 5. \]
(8) Teilen Sie eine Zahl $ N $ so in zwei Teile, dass das Dreifache des Quadrats eines Teils plus das Doppelte des Quadrats des anderen Teils ein Minimum ist.
(9) Der Wirkungsgrad u eines elektrischen Generators bei verschiedenen Leistungswerten x wird durch die folgende allgemeine Gleichung ausgedrückt:
\[ u=\frac{x}{a+bx+cx^2}; \]
wobei a eine Konstante ist, die hauptsächlich von den Energieverlusten im Eisen abhängt und c eine Konstante ist, die hauptsächlich vom Widerstand der Kupferteile abhängt. Finden Sie einen Ausdruck für den Wert der Ausgabe, bei dem die Effizienz maximal ist.
(10)Angenommen, es sei bekannt, dass der Kohleverbrauch eines bestimmten Dampfers durch die Formel $y = 0,3 + 0,001 v^3 $ dargestellt werden kann; Dabei ist y die Anzahl der Tonnen Kohle, die pro Stunde verbrannt wird und v ist die Geschwindigkeit ausgedrückt in Seemeilen pro Stunde. Die Kosten für Löhne, Kapitalzinsen und Abschreibung dieses Schiffes entsprechen zusammengenommen pro Stunde den Kosten von 1 Tonne Kohle. Bei welcher Geschwindigkeit werden die Gesamtkosten einer Reise von $1000 $ Seemeilen auf ein Minimum reduziert? Und wenn Kohle 10 Schilling pro Tonne kostet, wie hoch werden dann diese Mindestkosten der Reise sein?
(11) Bestimmen Sie Maxima und Minima von
\[ y = \pm\frac{x}{6}\sqrt{x(10-x)}. \]
(12) Bestimmen Sie Maxima und Minima von
\[ y= 4x^3 - x^2 - 2x + 1. \]
Antworten
(1) Max.: $x = -2,19$, $y = 24,19$; Min.:, $x = 1,52$, $y = -1,38$.
(2) $\dfrac{dy}{dx} = \dfrac{b}{a} - 2cx$; $\dfrac{d^2 y}{dx^2} = -2c$; $x = \dfrac{b}{2ac}$ (ein Maximum).
(3)
- (a ) Ein Maximum und zwei Minima.
- (b ) Ein Maximum. ($x = 0$; die anderen Punkte sind nicht real.)
(4) Min.: $x = 1,71$, $y = 6,14$.
(5) Max: $x = -0,5$, $y = 4$.
(6) Max.: $x = 1,414$, $y = 1,7675$. Min.: $x = -1,414$, $y = 1,7675$.
(7) Max.: $x = -3,565$, $y = 2,12$. Min.: $x = +3,565$, $y = 7,88$.
(8) $0,4N$, $0,6N$.
(9) $x = \sqrt{\dfrac{a}{c}}$.
(10) Geschwindigkeit $8,66$ nautische Meilen (Seemeilen) pro Stunde. Benötigte Zeit $115,47$ Stunden. Minimum Kosten ?$112$. 12s .
(11) Max. und min. für $x = 7,5$, $y = \pm 5,414$. (Siehe Beispiel Nr.10, hier.)
(12) Min.: $x = \frac{1}{2}$, $y= 0,25$; max.: $x = - \frac{1}{3}$, $y= 1,408$.