Volumina durch Integration

Was wir mit der Fläche eines kleinen Streifens einer Oberfläche gemacht haben, können wir natürlich genauso gut mit dem Volumen eines kleinen Streifens eines Körpers machen. Wir können alle kleinen Streifen, aus denen der gesamte Körper besteht, zusammenzählen und sein Volumen bestimmen, genau so wie wir alle kleinen Teile, aus denen sich eine Fläche zusammensetzt, addiert haben, um die endgültige Fläche der betrachteten Kurve / Abbildung zu finden.

Beispiele

(1) Bestimme das Volumen einer Kugel mit dem Radius r.

Eine dünne Kugelschale besitzt als Volumen $4\pi x^2\, dx$ (siehe Abbildung 59;). Summiert man alle konzentrischen Schalen auf, aus denen die Kugel besteht, so erhält man \[ \text{Volumen der Kugel} = \int^{x=r}_{x=0} 4\pi x^2\, dx = 4\pi \left[\frac{x^3}{3} \right]^r_0 = \tfrac{4}{3} \pi r^3. \]

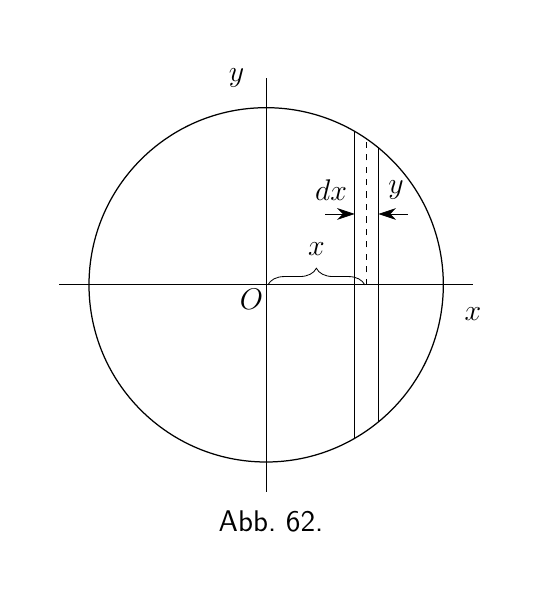
Wir können auch folgendermaßen vorgehen: Eine Scheibe der Kugel, mit der Dicke dx, hat ein Volumen von $\pi y^2\, dx$ (siehe Abbildung 62).

Auch gibt es zwischen x und y den folgenden Zusammenhang:

\[ y^2 = r^2 - x^2. \]

\begin{align*} \text{Volumen der Kugel} &= 2 \int^{x=r}_{x=0} \pi(r^2-x^2)\, dx \\ &= 2 \pi \left[ \int^{x=r}_{x=0} r^2\, dx - \int^{x=r}_{x=0} x^2\, dx \right] \\ &= 2 \pi \left[r^2x - \frac{x^3}{3} \right]^r_0 = \frac{4\pi}{3} r^3. \end{align*}

(2) Bestimmen Sie das Volumen des Körpers, das durch die Drehung der Kurve $y^2=6x$ um die x-Achse, zwischen $x=0$ und $x=4$, entsteht.

Das Volumen eines Streifens des Körpers ist $\pi y^2\, dx$. Daher ist das Volumen des Körpers

\begin{align*} \text{Volumen} &= \int^{x=4}_{x=0} \pi y^2\, dx = 6\pi \int^{x=4}_{x=0} x\, dx \\ &= 6\pi \left[ \frac{x^2}{2} \right]^4_0 = 48\pi = 150,8. \end{align*}