Flächen in Polarkoordinaten
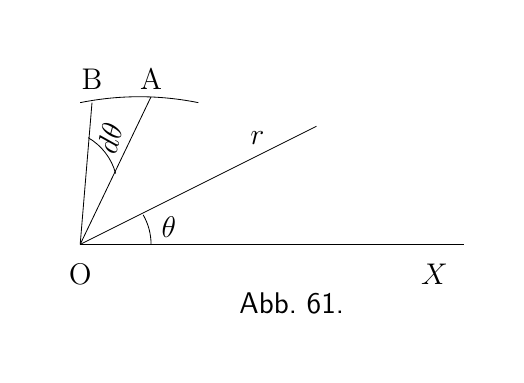
Wenn die Gleichung der Begrenzung einer Fläche als Funktion des Abstandes r eines Punktes davon von einem festen Punkt O (siehe Abbildung 61), der als Pol bezeichnet wird, und des Winkels, den r mit der positiven horizontalen Richtung OX bildet, gegeben ist, kann das soeben erläuterte Verfahren mit einer kleinen Modifikation genauso einfach angewendet werden.
Anstelle eines Flächenstreifens betrachten wir ein kleines Dreieck OAB, wobei der Winkel an O $d\theta$ ist, und wir finden die Summe aller kleinen Dreiecke, die die erforderliche Fläche bilden.
Der Flächeninhalt eines solchen kleinen Dreiecks ist ungefähr $\dfrac{AB}{2} \times r$ beziehungsweise $\dfrac{r\, d\theta}{2} \times r$; daher ist der Teil der Fläche, der zwischen der Kurve und zwei Positionen von r liegt, die den Winkeln $\theta_1$ und $\theta_2$ entsprechen, gegeben durch
\[ \tfrac{1}{2} \int^{\theta=\theta_2}_{\theta=\theta_1} r^2\, d\theta. \]
Beispiele
(1) Bestimmen Sie den Flächeninhalt des Kreissektors, bei dem der Kreisbogen 1 rad lang ist. Der Radius des Kreises ist a.
Die Polarkoordinaten des Umfangs (bzw. des Teils des Umfanges der zu dem untersuchten Kreisbogen gehört) ist offensichtlich $r=a$. Der Flächeninhalt ist
\[ \tfrac{1}{2} \int^{\theta=\theta_2}_{\theta=\theta_1} a^2\, d\theta = \frac{a^2}{2} \int^{\theta=1}_{\theta=0} d\theta = \frac{a^2}{2}. \]
(2) Finden Sie den Flächeninhalt des ersten Quadranten der Kurve (bekannt als pascalsche Schnecke), deren Polarkoordinaten $r=a(1+\cos \theta)$ sind.
\begin{align*} \text{Fläche} &= \tfrac{1}{2} \int^{\theta=\frac{\pi}{2}}_{\theta=0} a^2(1+\cos \theta)^2\, d\theta \\ &= \frac{a^2}{2} \int^{\theta=\frac{\pi}{2}}_{\theta=0} (1+2 \cos \theta + \cos^2 \theta)\, d\theta \\ &= \frac{a^2}{2} \left[\theta + 2 \sin \theta + \frac{\theta}{2} + \frac{\sin 2 \theta}{4} \right]^{\frac{\pi}{2}}_{0} \\ &= \frac{a^2(3\pi+8)}{8}. \end{align*}