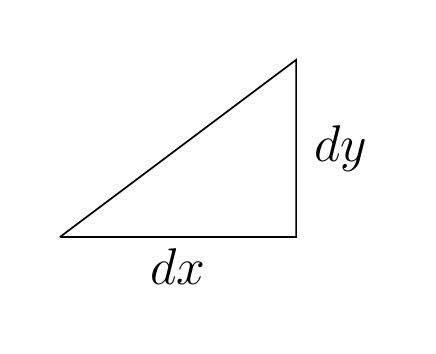Steigungen von Kurven und die Kurven selbst.
Lassen Sie uns eine kleine Vorüberlegung über die Steigungen von Kurven anstellen. Denn wir haben gesehen, dass das Differenzieren einer Kurve bedeutet, einen Ausdruck für ihre Steigung (oder für ihre Steigungen an verschiedenen Punkten) zu finden. Können wir den umgekehrten Prozess der Rekonstruktion der gesamten Kurve durchführen, wenn uns die Steigung (oder die Steigungen) vorgegeben sind?
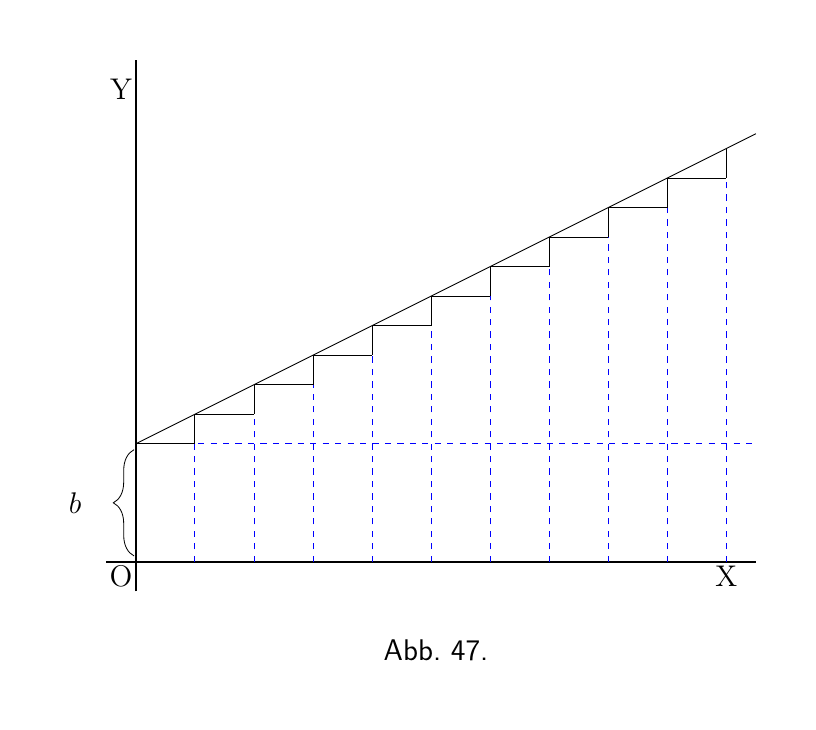
Gehen Sie zurück zu Fall (2) hier. Hier haben wir die einfachste aller Kurven, eine schräge Linie mit der Gleichung
\[ y = ax+b. \]
Wir wissen, dass hier b die Anfangshöhe von y bei $x= 0$ darstellt, und dass a, dass gleich $\dfrac{dy}{dx}$ ist, die Steigung der Geraden ist. Die Gerade hat eine konstante Steigung. Entlang der Geraden haben die elementaren Dreiecke
das gleiche Verhältnis zwischen Höhe und Grundseite. Nehmen wir an, dass die dx's und dy's von endlicher Größe sind, sodass 10 dx's einen Zentimeter ausmachen, dann gäbe es zehn kleine Dreiecke wie
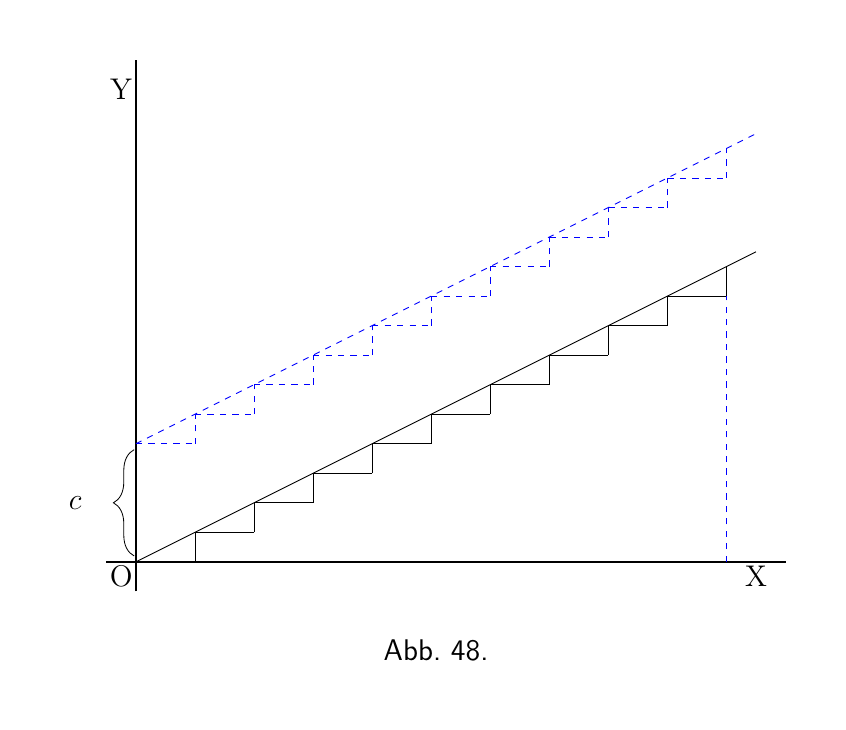
Nun nehmen wir an, wir hätten die Aufgabe, die Kurve zu rekonstruieren, indem wir lediglich von der Information ausgehen, dass $\dfrac{dy}{dx} = a$ ist. Was könnten wir tun? Nehmen wir weiterhin an, dass die kleinen d endlich groß sind, könnten wir 10 von ihnen (elementar Dreiecke) zeichnen, alle mit der gleichen Steigung, und sie dann aneinanderreihen, so wie hier:
Und da die Steigung für alle gleich ist, würden sie sich, wie in Abbildung 48, zu einer schrägen Linie mit der richtigen Steigung $\dfrac{dy}{dx} = a$ verbinden. Und ob wir die dy's und dx's als endlich oder unendlich klein nehmen, da sie alle gleich sind, ist eindeutig $\dfrac{y}{x} = a$, wenn wir y als die Summe aller dy's und x als die Summe aller dx's auffassen. Wo aber sollen wir diese schräge Linie ansetzen? Sollen wir am Ursprung $O$ beginnen, oder weiter oben? Da die einzige Information, die wir haben, die Steigung ist, haben wir keine Hinweise auf die bestimmte Höhe über $O$; in der Tat ist die Anfangshöhe unbestimmt. Die Steigung wird gleich sein, unabhängig von der Anfangshöhe. Machen wir also einen Versuch und beginnen wir die (steigende) Linie in einer Höhe $C$ über $O$. Das heißt, wir haben die Gleichung
\[ y = ax + C. \]
Es wird nun deutlich, dass in diesem Fall die hinzugefügte Konstante den bestimmten Wert meint, den y hat, wenn $x = 0$.
Nehmen wir nun einen schwierigeren Fall, nämlich den einer Geraden, deren Steigung nicht konstant ist, sondern immer mehr ansteigt. Nehmen wir an, dass die Steigung mit wachsendem x immer größer wird. Als Formel ist das:
\[ \frac{dy}{dx} = ax. \]
Oder, um einen konkreten Fall zu nennen, nehmen Sie $a = \frac{1}{5}$, so dass gilt
\[ \frac{dy}{dx} = \tfrac{1}{5} x. \]
Dann beginnen wir am besten damit, einige Werte der Steigung bei verschiedenen Werten von x zu berechnen und auch kleine Diagramme davon zu zeichnen.
Wenn
| $x =0$ | $ \frac{dy}{dx} = 0 $ |  |
| $x =1$ | $ \frac{dy}{dx} = 0,2 $ |  |
| $x =2$ | $ \frac{dy}{dx} = 0,4 $ |  |
| $x =3$ | $ \frac{dy}{dx} = 0,6 $ |  |
| $x =4$ | $ \frac{dy}{dx} = 0,8 $ |  |
| $x =5$ | $ \frac{dy}{dx} = 1,0 $ |  |
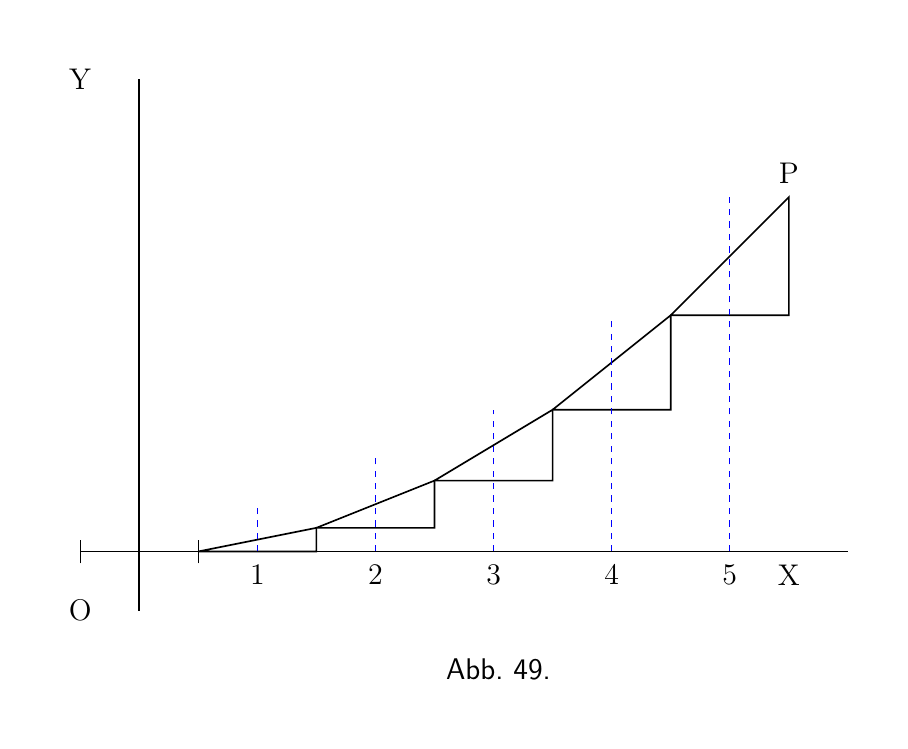
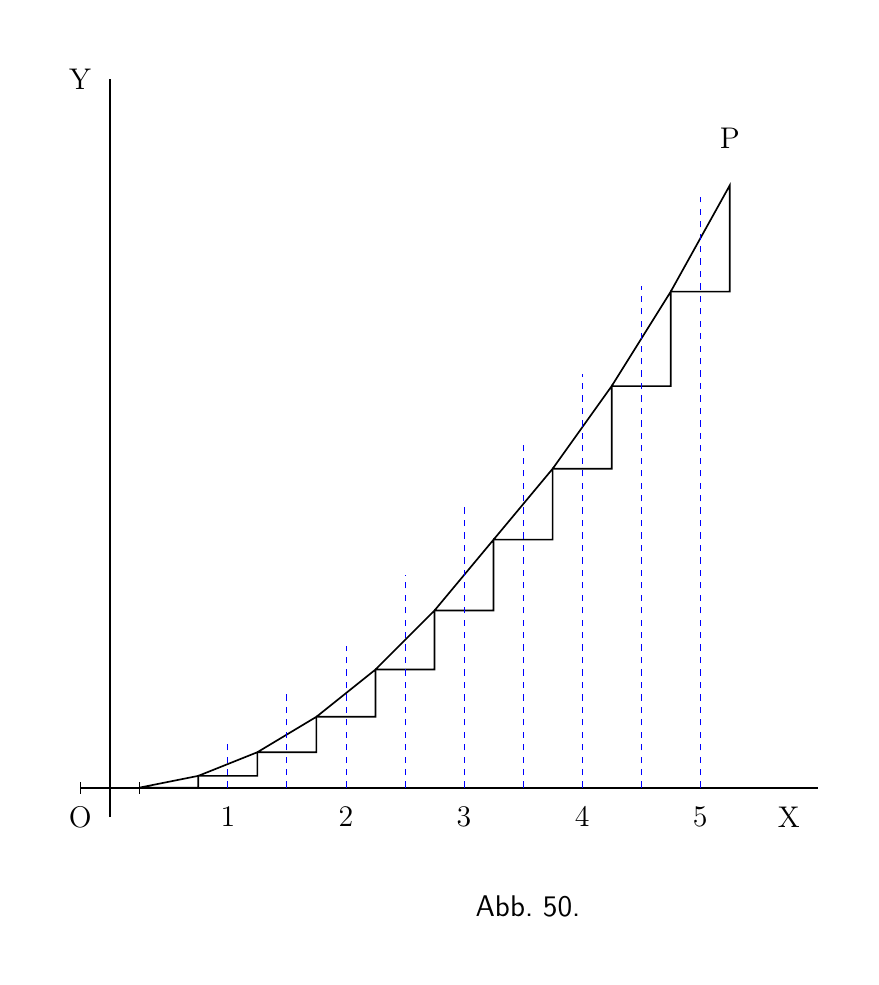
Versuchen Sie nun, die Teile so zusammenzusetzen, dass die Mitte ihrer Basis den richtigen Abstand nach rechts hat und dass sie an den Ecken zusammenpassen; also Abbildung 49. Das Ergebnis ist natürlich keine glatte Kurve, aber es ist eine Annäherung an eine solche. Hätten wir halb so lange und doppelt so viele Elemente / Teilstücke genommen, wie Abbildung 50, hätten wir eine bessere Annäherung. Aber für eine perfekte Kurve müssten wir jedes dx und sein entsprechendes dy unendlich klein und unendlich viele davon nehmen.
Wie groß soll dann der Wert eines beliebigen y sein? Es ist klar, dass an jedem Punkt P der Kurve der Wert von y die Summe aller kleinen dy von 0 bis zu dieser Höhe ist, also $\int dy = y$. Und da jedes dy gleich $\frac{1}{5}x \cdot dx$ ist, folgt daraus, dass das ganze y gleich der Summe all dieser Teilstücke wie $\frac{1}{5}x \cdot dx$ sein wird, oder, wie wir es schreiben sollten, $\int \tfrac{1}{5}x \cdot dx$.
Wenn nun x konstant gewesen wäre, wäre $\int \tfrac{1}{5}x \cdot dx$ dasselbe wie $\frac{1}{5} x \int dx$, oder $\frac{1}{5}x^2$ gewesen. Aber x begann mit 0 und steigt bis zu dem bestimmten Wert von x am Punkt P an, so dass sein Mittelwert von 0 bis zu diesem Punkt $\frac{1}{2}x$ ist. Daraus folgt $\int \tfrac{1}{5} x\, dx = \tfrac{1}{10} x^2$; oder $y=\frac{1}{10}x^2$.
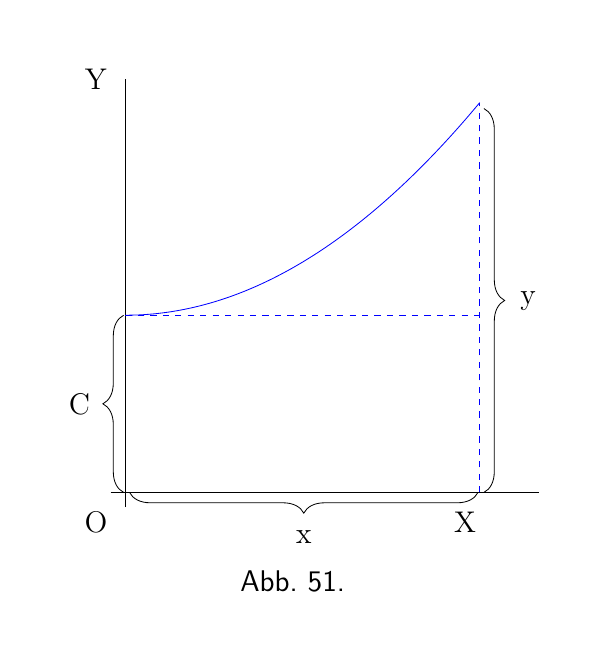
Aber auch hier müssen wir eine unbestimmte Konstante $C$ hinzufügen, weil wir nicht wissen, in welcher Höhe über dem Ursprung die Kurve beginnt, wenn $x = 0$ ist. Wir schreiben also, als Gleichung der in Abbildung 51 gezeichneten Kurve,
\[ y = \tfrac{1}{10}x^2 + C. \]
Übungen XVI
(1) Bestimmen Sie die Endsumme von $\frac{2}{3} + \frac{1}{3} + \frac{1}{6} + \frac{1}{12} + \frac{1}{24} + \text{etc}$.
(2) Zeigen Sie dass die Reihe $1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \frac{1}{5} - \frac{1}{6} + \frac{1}{7}$ etc., konvergent ist, und bestimmen Sie ihre Summe für die ersten $8$ Terme.
(3) Wenn $\log_\epsilon(1+x) = x - \dfrac{x^2}{2} + \dfrac{x^3}{3} - \dfrac{x^4}{4} + \text{etc}$ ist., bestimmen Sie $\log_\epsilon 1.3$.
(4) Bestimmen Sie y nach einer ähnlichen Argumentation wie in diesem Kapitel erläutert wurde, für den Fall
\[ (a) \text{wenn}\; \frac{dy}{dx} = \tfrac{1}{4} x; ? ? (b) \text{wenn}\; \frac{dy}{dx} = \cos x. \]
(5) Bestimmen Sie für $\dfrac{dy}{dx} = 2x + 3$, den Wert von y.
Antworten
(1) $1\frac{1}{3}$.
(2) $0,6344$.
(3) $0,2624$.
(4) (a ) $y = \frac{1}{8} x^2 + C$; ? ? (b ) $y = \sin x + C$.
(5) $y = x^2 + 3x + C$.