Integration

Das große Geheimnis ist schon gelüftet, dass dieses rätselhafte Symbol $\int$, das ja nur ein langes $S$ ist, nur die Summe von bedeutet, oder die Summe aller solchen Mengen wie. Es ähnelt also jenem anderen Symbol $\sum$ (dem griechischen Sigma), das ebenfalls ein Zeichen der Summation ist. Es gibt jedoch einen Unterschied in der Praxis der Mathematik, was den Gebrauch dieser Zeichen betrifft: Während $\sum$ im Allgemeinen verwendet wird, um die Summe einer Anzahl endlicher Mengen anzugeben, wird das Integralzeichen $\int$ im Allgemeinen verwendet, um die Summierung einer riesigen Anzahl kleiner Mengen von unbestimmter Größe anzugeben, eigentlich nur Elemente, die die erforderliche Summe ausmachen. So ist $\int dy = y$, und $\int dx = x$.

Jeder kann verstehen, wie das Ganze von irgendetwas als aus vielen kleinen Stücken bestehend aufgefasst werden kann; und je kleiner die Stücke sind, desto mehr von ihnen wird es geben. So kann man sich eine Linie, die einen Zentimeter lang ist, als aus 10 Teilen zusammengesetzt denken, von denen jedes $\frac{1}{10}$ eines Zentimeters lang ist; oder aus 100 Teilen, von denen jedes Teil $\frac{1}{100}$ eines Zentimeters lang ist; oder aus $1 000 000$ Teilen, von denen jedes $\frac{1}{1 000 000}$ eines Zentimeters lang ist; oder, den Gedanken bis an die Grenzen des Vorstellbaren treibend, kann es als aus einer unendlichen Anzahl von Elementen zusammengesetzt betrachtet werden, von denen jedes unendlich klein ist.

Ja, werden Sie sagen, aber was nützt es, etwas auf diese Weise zu betrachten? Warum kann man es nicht gleich als Ganzes betrachten? Der einfache Grund ist, dass es eine große Anzahl von Fällen gibt, in denen man die Größe der Sache als Ganzes nicht berechnen kann, ohne die Summe vieler kleiner Teile zusammenzurechnen. Der Prozess des Integrierens soll es uns ermöglichen, Summen zu berechnen, die wir sonst nicht direkt berechnen könnten.

Lassen Sie uns zunächst ein oder zwei einfache Fälle betrachten, um uns mit dem Begriff der Summierung vieler Einzelteile vertraut zu machen.

Betrachten Sie die Reihe:

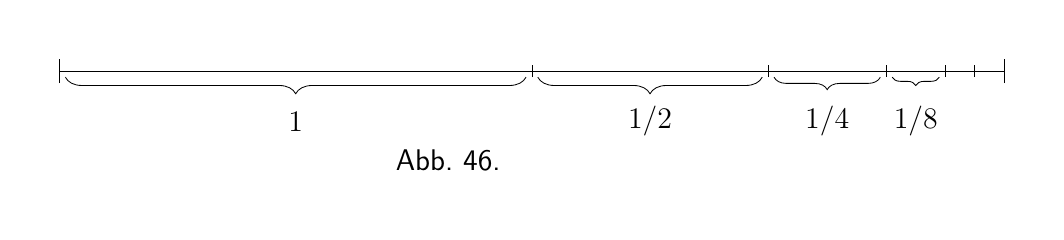
\[ 1 + \tfrac{1}{2} + \tfrac{1}{4} + \tfrac{1}{8} + \tfrac{1}{16} + \tfrac{1}{32} + \tfrac{1}{64} + \text{etc.} \]

Hier wird jedes Glied der Reihe gebildet, indem man ihm die Hälfte des Wertes des vorhergehenden nimmt. Wie hoch ist der Wert der Summe, wenn wir zu einer unendlichen Anzahl von Termen übergehen könnten? Jeder Schuljunge weiß, dass die Antwort 2 ist. Stellen Sie es sich, wenn Sie wollen, als eine Linie vor. Beginnen Sie mit einem Zentimeter; fügen Sie einen halben Zentimeter hinzu, fügen Sie ein Viertel hinzu, fügen Sie ein Achtel hinzu, und so weiter. Wenn wir an irgendeinem Punkt der Operation aufhören, wird es immer noch ein Stück geben, das die ganzen 2 Zentimeter ausmachen will; und das fehlende Stück wird immer die gleiche Größe haben wie das zuletzt hinzugefügte Stück. Wenn wir also, nachdem wir 1, $\frac{1}{2}$ und $\frac{1}{4}$ zusammengefügt haben, aufhören, so fehlt noch $\frac{1}{4}$. Wenn wir weitermachen, bis wir $\frac{1}{64}$ addiert haben, wird immer noch $\frac{1}{64}$ fehlen. Der benötigte Rest ist immer gleich dem zuletzt hinzugefügten Term. Nur durch eine unendliche Anzahl von Operationen sollten wir die tatsächliche 2-Zahl erreichen. Praktisch sollten wir sie erreichen, wenn wir zu Stücken kommen, die so klein sind, dass sie nicht gezeichnet werden können - das wäre nach etwa 10 Termen, denn der elfte Term ist $\frac{1}{1024}$. Wenn wir so weit gehen wollen, dass nicht einmal eine Whitworth'sche Messmaschine sie erkennen würde, müssten wir nur bis etwa $20$ Terme gehen. Ein Mikroskop würde nicht einmal den 18ten-Term anzeigen! Die unendliche Anzahl von Operationen ist also doch keine so furchtbare Sache. Das Integral ist einfach die ganze Menge. Aber, wie wir sehen werden, gibt es Fälle, in denen die Integralrechnung es ermöglicht, auf die exakte Summe zu kommen, die sich als Ergebnis einer unendlichen Anzahl von Operationen ergeben würde. In solchen Fällen gibt uns die Integralrechnung einen schnellen und einfachen Weg, um zu einem Ergebnis zu kommen, das sonst eine unendliche Menge an aufwändiger Ausarbeitung erfordern würde. Wir sollten also keine Zeit verlieren, um zu lernen, wie man integriert.