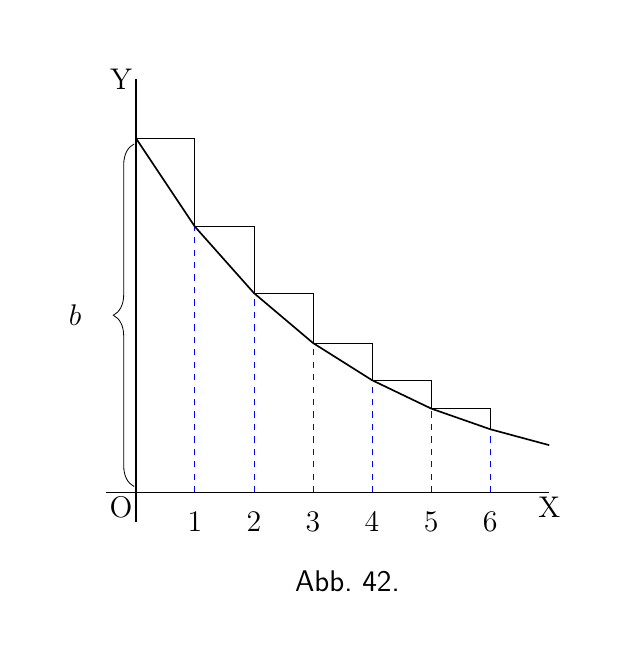
Die Zerfallskurve
Wenn wir annehmen dass es sich bei $p$ um einen echten Bruch, weniger als eins, handelt, würde die Kurve offensichtlich dazu neigen, nach unten zu sinken, wie in Abbildung 42, wobei jede aufeinanderfolgende Ordinate $\frac{3}{4}$ der Höhe der vorhergehenden entspricht.
Die Gleichung ist immer noch:
\[ y=bp^x; \]
da aber $p$ kleiner als eins ist, wird $\log_\epsilon p$ eine negative Größe sein und kann als $-a$ geschrieben werden; so dass $p=\epsilon^{-a}$ ist, und jetzt hat unsere Gleichung, für die Kurve, die Form
\[ y=b\epsilon^{-ax}. \]
Die Bedeutung dieses Ausdrucks besteht darin, dass für den Fall, dass die unabhängige Variable Zeit ist, die Gleichung den Verlauf vieler physikalischer Prozesse darstellt, bei denen etwas abnimmt. Somit wird die Abkühlung eines heißen Körpers (in Newtons berühmtem Gesetz der Abkühlung) durch die Gleichung:
\[ \theta_t=\theta_0 \epsilon^{-at} \text{ beschrieben;} \]
wobei $\theta_0$ der ursprüngliche Temperaturüberschuss eines heißen Körpers gegenüber seiner Umgebung ist, $\theta_t$ der Temperaturüberschuss am Ende der Zeit t und a eine Konstante ist, nämlich, die Abnahmekonstante, abhängig von der vom Körper exponierten Oberfläche und von seinen Leitfähigkeits- und Emissionsgrad usw.
Ein ähnlich Formel ist:
\[ Q_t=Q_0 \epsilon^{-at}, \]
diese wird verwendet, um die Ladung eines elektrifizierten Körpers auszudrücken, der ursprünglich eine Ladung $Q_0$ hatte, die mit einer abnehmenden Konstanten a entweicht; welche Konstante hängt in diesem Fall von der Kapazität des Körpers und vom Widerstand der Kriechstrecke (Kriechstrecke ist definiert als kürzeste Entfernung entlang der Oberfläche eines Isolierstoffes zwischen zwei leitenden Teilen) ab. Es handelt sich dabei um die Entladung eines Kondensators über einen Widerstand
Schwingungen einer flexiblen Feder klingen nach einiger Zeit ab; und das Abklingen der Bewegungsamplitude kann auf ähnliche Weise ausgedrückt werden.
Tatsächlich dient $\epsilon^{-at}$ als Abklingfaktor für all jene Phänomene, bei denen die Abnahmerate proportional zur Größe der Abnahme ist; oder wo, in unseren üblichen Symbolen, $\dfrac{dy}{dt}$ zu jedem Zeitpunkt proportional zu dem Wert ist, den y gerade hat. Denn wir müssen nur die Kurve untersuchen, Abbildung 42 oben, um zu sehen, dass die Steigung $\dfrac{dy}{dx}$ an jedem Teil davon proportional ist zur Höhe y; die Kurve wird flacher, wenn y kleiner wird. In Symbolen, also
$y=b\epsilon^{-ax}$ or \[ \log_\epsilon y = \log_\epsilon b - ax \log_\epsilon \epsilon = \log_\epsilon b - ax,\\ \text{und, differenzieren, }\; \frac{1}{y}\, \frac{dy}{dx} = -a;\\ \text{daher }\; \frac{dy}{dx} = b\epsilon^{-ax} \times (-a) = -ay; \]
oder, in Worten, die Steigung der Kurve ist nach unten gerichtet und proportional zu y und zur Konstanten a.
Wir hätten das gleiche Ergebnis erhalten, wenn wir die Gleichung in der folgenden Form genommen hätten
\begin{align*} y &= bp^x; \\ \text{für }\; \frac{dy}{dx} &= bp^x \times \log_\epsilon p. \\ \text{aber }\; \log_\epsilon p &= -a; \\ \text{gibt uns }\; \frac{dy}{dx} &= y \times (-a) = -ay, \end{align*}
wie zuvor.
Die Zeitkonstante. Im Ausdruck für den Abnahmefaktor / Zerfallsfaktor $\epsilon^{-at}$ ist die Größe a der Kehrwert von einer anderen Größe, die als Zeitkonstante bekannt ist und die wir mit dem Symbol T bezeichnen können. Dann lautet der Abnahmefaktor $\epsilon^{-\frac{t}{T}}$; indem man $t = T$ setzt, erkennt man die Bedeutung von T bzw. von $\dfrac{1}{a}$, es handelt sich hierbei um die Zeitlänge, die es braucht, damit die ursprüngliche Menge (in den vorhergehenden Fällen $\theta_0$ oder $Q_0$ genannt) den $\dfrac{1}{\epsilon}$ten Teil - das heißt, auf $0,3678$ - ihres ursprünglichen Wertes abnimmt.
Die Werte von $\epsilon^x$ und $\epsilon^{-x}$ werden in verschiedenen Bereichen der Physik ständig benötigt, und da sie in sehr wenigen Sätzen mathematischer Tabellen angegeben sind, sind einige der Werte hier aus Bequemlichkeit tabellarisch aufgeführt.
?
| x | $\epsilon^x$ | $\epsilon^{-x}$ | $1-\epsilon^{-x}$ |
|---|---|---|---|
| 0 | $1.0000$ | $1.0000$ | $0.0000$ |
| $0.10$ | $1.1052$ | $0.9048$ | $0.0952$ |
| $0.20$ | $1.2214$ | $0.8187$ | $0.1813$ |
| $0.50$ | $1.6487$ | $0.6065$ | $0.3935$ |
| $0.75$ | $2.1170$ | $0.4724$ | $0.5276$ |
| $0.90$ | $2.4596$ | $0.4066$ | $0.5934$ |
| $1.00$ | $2.7183$ | $0.3679$ | $0.6321$ |
| $1.10$ | $3.0042$ | $0.3329$ | $0.6671$ |
| $1.20$ | $3.3201$ | $0.3012$ | $0.6988$ |
| $1.25$ | $3.4903$ | $0.2865$ | $0.7135$ |
| $1.50$ | $4.4817$ | $0.2231$ | $0.7769$ |
| $1.75$ | $5.755$ | $0.1738$ | $0.8262$ |
| $2.00$ | $7.389$ | $0.1353$ | $0.8647$ |
| $2.50$ | $12.182$ | $0.0821$ | $0.9179$ |
| $3.00$ | $20.086$ | $0.0498$ | $0.9502$ |
| $3.50$ | $33.115$ | $0.0302$ | $0.9698$ |
| $4.00$ | $54.598$ | $0.0183$ | $0.9817$ |
| $4.50$ | $90.017$ | $0.0111$ | $0.9889$ |
| $5.00$ | $148.41$ | $0.0067$ | $0.9933$ |
| $5.50$ | $244.69$ | $0.0041$ | $0.9959$ |
| $6.00$ | $403.43$ | $0.00248$ | $0.99752$ |
| $7.50$ | $1808.04$ | $0.00055$ | $0.99947$ |
| $10.00$ | $22026.5$ | $0.000045$ | $0.999955$ |
Als Beispiel für die Verwendung dieser Tabelle nehmen wir an, es gibt eine Abkühlung des heißen Körpers und zu Beginn des Experiments (d.h. zum Zeitpunkt t = 0) ist der Körper $72^{\circ}$ heißer als die umgebenden Objekte und wenn die Zeitkonstante seiner Abkühlung $20$ Minuten beträgt (d.h. wenn es $20$ Minuten dauert, bis der Temperaturüberschuss auf $\dfrac{1}{\epsilon}$ Teil von $72^{\circ}$ gefallen ist), dann können wir berechnen, auf welche Temperatur er nach einer bestimmten Zeit gefallen seien wird. Lassen Sie t beispielsweise 60 Minuten sein. Dann $\dfrac{t}{T} = 60 \div 20 = 3$, und wir müssen den Wert von $\epsilon^{-3}$ finden, und dann die ursprünglichen $72^{\circ}$ damit multiplizieren. Die Tabelle zeigt, dass $\epsilon^{-3}$ $0,0498$ ist. Nach 60 Minuten wird der Temperaturüberschuss also auf $72^{\circ} \times 0,0498 = 3,586^{\circ}$ gefallen sein.
Weitere Beispiele.
(1) Die Stärke eines elektrischen Stroms in einem Leiter zu einem Zeitpunkt t sek nach dem Aufbringen der sie erzeugenden elektromotorischen Kraft ergibt sich, durch den Ausdruck $C = \dfrac{E}{R}\left\{1 - \epsilon^{-\frac{Rt}{L}}\right\}$ .
Die Zeitkonstante ist $\dfrac{L}{R}$.
Wenn $E = 10$, $R =1$, $L = 0,01$; dann wenn t sehr groß ist, wird der Term $\epsilon^{-\frac{Rt}{L}}$ 1 werden und $C = \dfrac{E}{R} = 10$; also:
\[ \frac{L}{R} = T = 0.01. \]
Der Wert zu jedem Zeitpunkt kann so geschrieben werden:
\[ C = 10 - 10\epsilon^{-\frac{t}{0,01}}, \]
Die Zeitkonstante ist $0,01$. Das bedeutet, dass es $0,01$ Sek dauert bis der variable Term auf $\dfrac{1}{\epsilon} = 0.3678$ seines ursprünglichen Wertes von $10\epsilon^{-\frac{0}{0,01}} = 10$ gefallen ist.
Um den Wert des Stroms im Zeitpunkt $t = 0,001 \text{Sek}$ zu ermitteln, setzen wir $\dfrac{t}{T} = 0,1$, $\epsilon^{-0,1} = 0,9048$ (aus der Tabelle).
p>Daraus folgt, dass nach $0,001$ Sek. der variable Term $0,9048 \times 10 = 9,048$ beträgt und der Strom zu diesem Zeitpunkt $10 - 9,048 = 0,952$ beträgt.
In ähnlicher Weise, am Ende von $0,1$ Sek.
\[ \frac{t}{T} = 10;\quad \epsilon^{-10} = 0,000045; \]
Der variable Term ist $10 \times 0,000045 = 0,00045$, und der Strom ist $9,9995$.
(2) Die Intensität $I$ eines Lichtstrahls, der eine Dicke l cm eines transparenten Mediums durchquert hat, ist $I = I_0\epsilon^{-Kl}$, wobei $I_0$ die Anfangsintensität des Strahls und $K$ eine Absorptionskonstante ist.
Diese Konstante wird normalerweise durch Experimente bestimmt. Wenn beispielsweise festgestellt wird, dass die Intensität eines Lichtstrahls sich beim Durchgang durch 10 cm, eines bestimmten transparenten Mediums, um 18% verringert, bedeutet dies das $82 = 100 \times \epsilon^{-K \times 10}$ ist beziehungsweise $\epsilon^{-10K} = 0,82$, und in der Tabelle findet man $10K = 0,20$ (fast); daher $K = 0,02$.
Um die Dicke zu finden, die die Intensität auf die Hälfte reduziert, muss man den Wert von l finden, der die Gleichung $50 = 100 \times \epsilon^{-0,02l}$ oder $0,5 = \epsilon^{-0,02l}$ erfüllt. Sie wird gefunden, indem man diese Gleichung in ihre logarithmische Form setzt, nämlich:
\[ \log 0.5 = -0.02 \times l \times \log \epsilon, \]
was Folgendes ergibt:
\[ l = \frac{-0.3010}{-0.02 \times 0.4343} = 34.7 \text{cm (ungefähr)}. \]
(3) Die (verbliebene) Menge Q eines radioaktiven Stoffes, die noch nicht zerfallen ist, steht mit der ursprünglich (vorhandenen) Menge $Q_0$ der Substanz in Beziehung. Der Zusammenhang zwischen den Mengen Q und $Q_0$ lässt sich, durch die Gleichung $Q = Q_0 \epsilon^{-\lambda t}$ beschreiben, wobei $\lambda$ eine Konstante ist und t für die Zeit in Sekunden steht, die seit dem Beginn des Zerfallsprozesses vergangen ist.
Für Radium A zeigt das Experiment, wenn die Zeit in Sekunden ausgedrückt wird, dass $\lambda = 3,85 \times 10^{-3}$ ist. Bestimmen Sie die Zeit, die für den Zerfall der Hälfte der Substanz benötigt wird. (Diese Zeit wird als mittlere Lebensdauer der Substanz bezeichnet.)
Wir haben $0,5 = \epsilon^{-0,00385t}$.
\begin{align*} \log 0,5 &= -0,00385t \times \log \epsilon; \\ \text{und }\; t &= 3\text{ Minuten (fast)}. \end{align*}
Übungen XIII
(1) Zeichnen Sie die Kurve von $y = b \epsilon^{-\frac{t}{T}}$; für $b = 12$, $T = 8$ und t mit verschiedene Werten von 0 bis $20$.
(2) Wenn ein heißer Körper so abkühlt, dass sein Temperaturüberschuss in 24Minuten auf die Hälfte des ursprünglichen Betrags gefallen ist, leiten Sie die Zeitkonstante ab und bestimmen Sie, wie lange es dauert bis er sich auf 1 Prozent des ursprünglichen Überschusses abgekühlt hat.
(3) Zeichnen Sie die Kurve von $y = 100(1-\epsilon^{-2t})$.
(4) Die folgenden Gleichungen ergeben sehr ähnliche Kurven:
\begin{align*} \text{(i)}\ y &= \frac{ax}{x + b}; \\ \text{(ii)}\ y &= a(1 - \epsilon^{-\frac{x}{b}}); \\ \text{(iii)}\ y &= \frac{a}{90^{\circ}} \arctan \left(\frac{x}{b}\right). \end{align*}
Zeichnen Sie alle drei Kurven, mit $a= 100$ Millimeter; $b = 30$ Millimeter.
(5) Bestimmen Sie den Differential Koeffizienten von y bezüglich x, für die folgenden drei Gleichungen:
\[ (a) y = x^x;\quad (b) y = (\epsilon^x)^x;\quad (c) y = \epsilon^{x^x}. \]
(6) Für Thorium A beträgt der Wert von $\lambda$ 5; bestimmen Sie die mittlere Lebensdauer, d.h. die Zeit, die für den Zerfall einer Menge Q von Thorium A auf die Hälfte der Anfangsmenge $Q_0$ benötigt wird, mit Hilfe des folgenden Ausdrucks:
\[ Q = Q_0 \epsilon^{-\lambda t}; \]
t ist in Sekunden.
(7) Ein Kondensator mit der Kapazität $K = 4 \times 10^{-6}$, wird auf ein Potential $V_0 = 20$ aufgeladen, und entlädt sich über einen Widerstand von $10 000$ Ohm. Bestimmen Sie das Potential V nach (a ) $0,1$ Sekunde; (b ) $0,01$ Sekunde; unter der Annahme, dass der Potentialabfall der Regel $V = V_0 \epsilon^{-\frac{t}{KR}}$ folgt.
(8) Die Ladung Q einer elektrifizierten isolierten Metallkugel wird in 10 Minuten von $20$ auf $16$ Einheiten reduziert. Bestimmen Sie den Koeffizienten $\mu$ der Entladung, wenn $Q = Q_0 \times \epsilon^{-\mu t}$; und $Q_0$ die anfängliche Ladung und t in Sekunden ist. Bestimmen Sie die Zeitdauer, die benötigt wird, bis sich die Ladung auf die Hälfte der ursprünglichen Ladung reduziert hat.
(9) Die Dämpfung einer Telefonleitung lässt sich, aus der Beziehung $i = i_0 \epsilon^{-\beta l}$ ermitteln, wobei i die Stärke des Telefonstroms nach t Sekunden, bei einer anfänglichen Stärke von $i_0$, ist. l ist die Länge der Leitung in Kilometern und $\beta$ ist eine Konstante. Für das 1910 verlegte französisch-englische Unterseekabel gilt $\beta = 0,0114$. Bestimmen Sie die Dämpfung am Ende des Kabels ($40$ Kilometer) und die Länge, auf der i noch $8$% des ursprünglichen Stroms beträgt (Grenzwert für sehr gutes Hören).
(10) Der Druck $p$ der Atmosphäre in einer Höhe h Kilometer, wird durch $p=p_0 \epsilon^{-kh}$ beschrieben; wobei $p_0$ der Druck auf Meereshöhe ($760$ Millimeter) ist.
Die Drücke bei 10 , $20 $ und $50 $ Kilometern betragen jeweils $ 199,2 $, $ 42,2 $ bzw. $ 0,32 $. Ermitteln Sie mit dem Mittelwert von k jeweils den prozentualen Fehler.
(11) Bestimmen Sie das Minimum oder Maximum von $y = x^x$.
(12) Bestimmen Sie das Minimum oder Maximum von $y = x^{\frac{1}{x}}$.
(13) Bestimmen Sie das Minimum oder Maximum von $y = xa^{\frac{1}{x}}$.
?
Antworten
(1) Sei $\dfrac{t}{T} = x$ ($\therefore t = 8x$), und benutzen Sie die obige Tabelle.
(2) $T = 34,627$; $159,46$ Minuten.
(3) Setzen Sie $2t = x$; und benutzen Sie die obige Tabelle.
(5) (a) $x^x \left(1 + \log_\epsilon x\right)$; ? ? (b ) $2x(\epsilon^x)^x$; ? ? (c ) $\epsilon^{x^x} \times x^x \left(1 + \log_\epsilon x\right)$.
(6) $0,14$ Sekunden.
(7) (a) $1,642$; ? ? (b) $15,58$.
(8) $\mu = 0,00037$; $31^m \frac{1}{4}$.
(9) i ist $63,4$% von $i_0$, $220$ Kilometer.
(10) $0,133$; $0,145$; $0,155$, Mittelwert $0,144$; $-10,2$%; $-0,9$%; $+77,2$%.
(11) Minimum für $x = \dfrac{1}{\epsilon}$.
(12) Maximum für $x = \epsilon$.
(13) Minimum für $x = \log_\epsilon a$.