Die logarithmische Kurve.

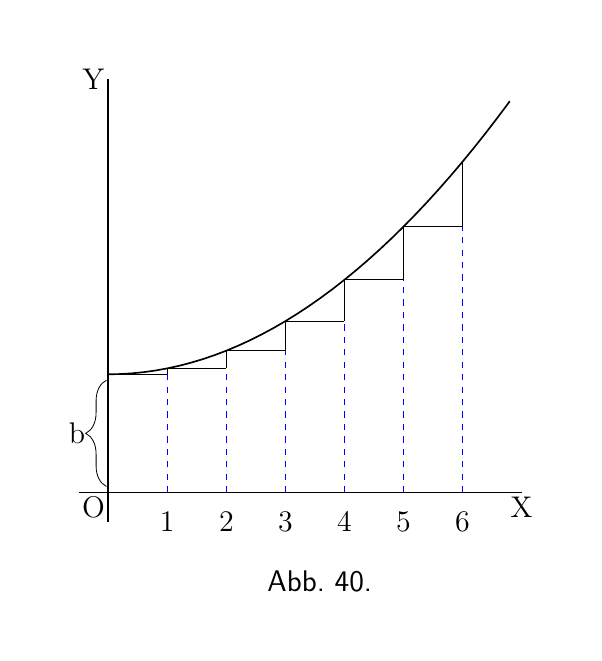
Kehren wir zu der Kurve zurück, die ihre aufeinanderfolgenden Ordinaten in geometrischer Abfolge hat, wie sie beispielsweise durch die Gleichung $y=bp^x$ dargestellt wird.

Wir können sehen, indem wir $x=0$ setzen, dass b die Anfangshöhe von y ist.

Dann, wenn

\[ x=1,\quad y=bp;\qquad x=2,\quad y=bp^2;\qquad x=3,\quad y=bp^3,\quad \text{etc.} \]

Außerdem sehen wir, dass $p$ der numerische Wert des Verhältnisses zwischen der Höhe einer beliebigen Ordinate und der der nächsthöheren ist. In Abbildung 40 haben wir angenommen das $p$ $\frac{6}{5}$ ist; jede Ordinate ist $\frac{6}{5}$ so hoch wie die vorhergehende.

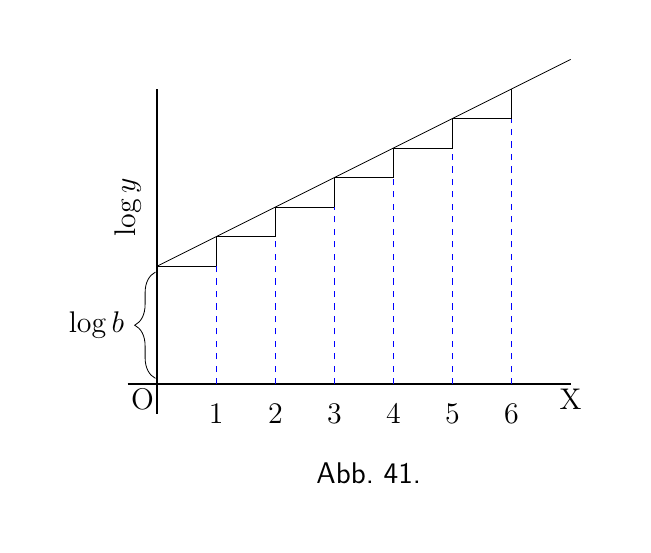
Wenn zwei aufeinanderfolgende Ordinaten also in einem konstanten Verhältnis zueinanderstehen, haben ihre Logarithmen eine konstante Differenz; wenn wir also eine neue Kurve zeichnen sollten, Abbildung 41, mit Werten von $\log_\epsilon y$ als Ordinate, wäre dies eine gerade Linie mit einer Steigung von gleiche Schritte. Tatsächlich folgt aus der Gleichung, dass:

\begin{align*} \log_\epsilon y &= \log_\epsilon b + x \cdot \log_\epsilon p, \\ \text{daher }\; \log_\epsilon y &- \log_\epsilon b = x \cdot \log_\epsilon p. \end{align*}

Da $\log_\epsilon p$ bloß eine Zahl ist und als $\log_\epsilon p=a$ geschrieben werden kann, folgt daraus

\[ \log_\epsilon \frac{y}{b}=ax, \]

und die Gleichung nimmt die neue Form an

\[ y = b\epsilon^{ax}. \]