Über den wahren Zinseszins und das Gesetz des organischen Wachstums

Es gebe eine Menge, die so wächst, dass der Zuwachs ihres Wachstums während einer bestimmten Zeit immer proportional zu ihrer eigenen Größe ist. Dies ähnelt dem Verfahren, Zinsen für Geld zu einem festen Zinssatz zu berechnen; denn je größer das Kapital, desto höher die Zinsen in einer bestimmten Zeit.

Nun müssen wir bei unserer Berechnung deutlich zwischen zwei Fällen unterscheiden, je nachdem die Berechnung durch das erfolgt, was die Rechenbücher einfachen Zins nennen, oder durch das, was sie Zinseszins nennen. Denn im ersten Fall bleibt das Kapital fest, während im letztem die Zinsen dem Kapital hinzugefügt werden, das sich also durch aufeinanderfolgende Hinzufügungen erhöht.

Zum einfachen Zins. Betrachten Sie einen konkreten Fall. Lassen Sie das Kapital zu Beginn 100 Euro sein, und lassen Sie den Zinssatz 10 Prozent pro Jahr sein. Dann beträgt der Zuwachs für den Eigentümer des Kapitals 10 Euro jedes Jahr. Lassen Sie ihn weiterhin jedes Jahr seine Zinsen beziehen und sie horten, indem er sie in einen Strumpf steckt oder in seinem Safe einschließt. Wenn er dann 10 Jahre lang weitermacht, wird er am Ende dieser Zeit 10 Teilbeträge von je 10 Euro beziehungsweise in Summe 100 Euro erhalten haben, was zusammen mit den ursprünglichen 100 Euro eine Summe von 2 Euro ergibt. Sein Vermögen wird sich in 10 Jahren verdoppelt haben. Wäre der Zinssatz 5 Prozent gewesen, hätte er $20$ Jahre lang horten müssen, um sein Vermögen zu verdoppeln. Wäre er nur 2 Prozent gewesen, hätte er $50$ Jahre lang horten müssen. Es ist leicht, einzusehen, dass er, wenn der Wert der jährlichen Zinsen $\dfrac{1}{n}$ des Kapitals beträgt, n Jahre lang weiter horten muss, um sein Vermögen zu verdoppeln.

Wenn y die ursprüngliche Summe des Kapitals ist, und der jährliche Zins ist $\dfrac{y}{n}$, dann wird am Ende von n Jahren sein Vermögen:

\[ y + n\dfrac{y}{n} = 2y \text{ betragen.} \]

(2) Mit Zinseszins. Wie zuvor, so möge der Eigentümer auch hier mit einem Kapital von 100 Euro beginnen, das jährlich mit 10 Prozent verzinst wird; aber, anstatt die Zinsen zu horten, möge man sie jedes Jahr dem Kapital hinzufügen, so dass das Kapital von Jahr zu Jahr wächst. Dann, am Ende des ersten Jahres, wird das Kapital auf $110$ Euro angewachsen sein; und im zweiten Jahr (immer noch zu 10%) wird dieses (gewachsene) Kapital $11$ Euro Zinsen einbringen. Der Eigentümer wird das dritte Jahr mit $121$ Euro beginnen, und die Zinsen darauf werden $12,1$ Euro betragen; so dass er das vierte Jahr mit $133,1$ Euro beginnt, und so weiter. Es ist leicht, auszurechnen, dass am Ende der zehn Jahre das Gesamtkapital auf $259,37$ Euro gewachsen sein wird. In der Tat sehen wir, dass am Ende eines jeden Jahres jeder Euro $\tfrac{1}{10}$ Euro eingebracht hat, und daher, wenn dies immer weiter addiert und jedes Jahr das Kapital mit dem Faktor $\tfrac{11}{10}$ multipliziert wird; und wenn es für zehn Jahre fortgesetzt wird, d.h. es wird zehnmal mit diesem Faktor multipliziert, wird das ursprüngliche Kapital mit $2,59374$ multipliziert. Lassen Sie uns dies in Symbole umsetzen. Setzen Sie $y_0$ für das ursprüngliche Kapital; $\dfrac{1}{n}$ für den Bruchteil, der bei jeder der n Operationen (Multiplikation mit dem Faktor) hinzukommt; und $y_n$ für den Wert des Kapitals am Ende der n-ten Operation. Dann ergibt sich folgender Ausdruck:

\[ y_n = y_0\left(1 + \frac{1}{n}\right)^n. \]

Aber diese Art, den Zinseszins einmal im Jahr zu berechnen, ist wirklich nicht ganz gerecht; denn schon im ersten Jahr hätten die 100 Euro wachsen müssen. Am Ende eines halben Jahres hätten es mindestens $105$ Euro sein müssen, und es wäre sicherlich gerechter gewesen, wenn die Zinsen für die zweite Jahreshälfte auf $105$ Euro berechnet worden wären. Dies wäre gleichbedeutend damit, dass man von 5% pro Halbjahr; und $20$ Operationen bei denen das Kapital jeweils mit $\tfrac{21}{20}$ multipliziert wird, ausgeht. Wenn auf diese Weise gerechnet wird, würde das Kapital am Ende von zehn Jahren auf $265,32$ Euro angewachsen sein; da

\[ (1 + \tfrac{1}{20})^{20} = 2,653. \]

Aber selbst dann ist der Vorgang noch nicht ganz gerecht; denn am Ende des ersten Monats wird ein gewisser Zins erwirtschaftet sein; und eine halbjährliche Rechnung setzt voraus, dass das Kapital jeweils sechs Monate lang fest bleibt. Nehmen wir an, wir teilen das Jahr in 10 Teile und rechnen für jedes Zehntel des Jahres einen Zins von einem Prozent (1\%). Wir haben nun 100 Operationen, die sich über die zehn Jahre erstrecken; oder

\[ y_n = 100 \text{Euro }\left( 1 + \tfrac{1}{100} \right)^{100}; \]

was $270,48$ Euro ergibt.

Aber das ist noch nicht das Ende. Lassen Sie uns die Jahre in $1000$ Perioden teilen, wobei jede $\frac{1}{100}$ von einem Jahr sei; der Zins für eine solche Periode ist dann $\frac{1}{10}$ Prozent beziehungsweise 1 Promille; dann

\[ y_n = 100 \text{Euro }\left( 1 + \tfrac{1}{1000} \right)^{1000}; \]

was $271,69$ Euro ergibt.

Gehen Sie noch weiter ins Detail und teilen Sie die zehn Jahre in $10.000$ Teile, jedes $\frac{1}{1000}$ eines Jahres, mit Zinsen von $\frac{1}{100}$ von 1 Prozent. Dann

\[ y_n = 100 \text{Euro }\left( 1 + \tfrac{1}{10,000} \right)^{10,000} \]

beträgt $271,81$ Euro.

Schließlich wird man sehen, dass das, was wir zu finden versuchen, in Wirklichkeit der letzte Wert des Ausdrucks $\left(1 + \dfrac{1}{n}\right)^n$ ist, der, wie wir sehen, größer als 2 ist; und der, wenn wir n größer und größer nehmen, einem bestimmten Grenzwert immer näher kommt. Wie groß man auch immer n macht, der Wert dieses Ausdrucks kommt der Zahl immer näher:

\[ 2.71828\ldots \]

eine Zahl, die Sie nicht vergessen dürfen.

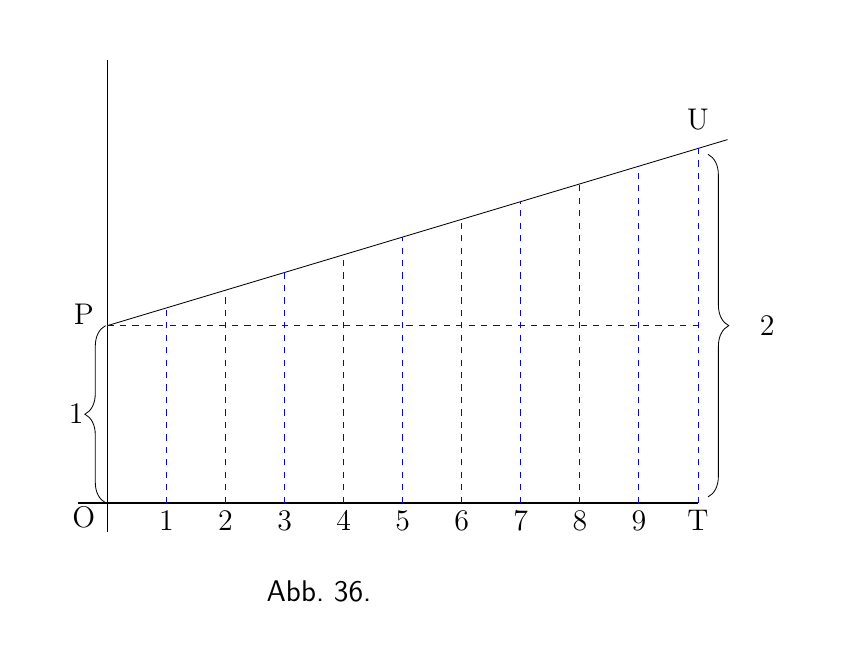
Lassen Sie uns diese Dinge geometrisch veranschaulichen. In Abbildung 36 steht $OP$ für den ursprünglichen Wert. $OT$ ist die gesamte Zeit, in der der Wert wächst. Sie ist in 10 Perioden unterteilt, in denen jeweils ein gleicher Schritt nach oben erfolgt. Hier ist $\dfrac{dy}{dx}$ eine Konstante; und wenn jeder Schritt nach oben $\frac{1}{10}$ des ursprünglichen $OP$ ist, dann wird durch 10 solcher Schritte die Höhe verdoppelt. Hätten wir $20$ Schritte gemacht, jeder von der Hälfte der gezeigten Höhe, so wäre am Ende die Höhe immer noch gerade verdoppelt. Oder n solche Schritte, jeder von $\dfrac{1}{n}$ der ursprünglichen Höhe $OP$, würden ausreichen, um die Höhe zu verdoppeln. Dies ist der Fall des einfachen Zinses. Hier wächst 1, bis es zu 2 wird.

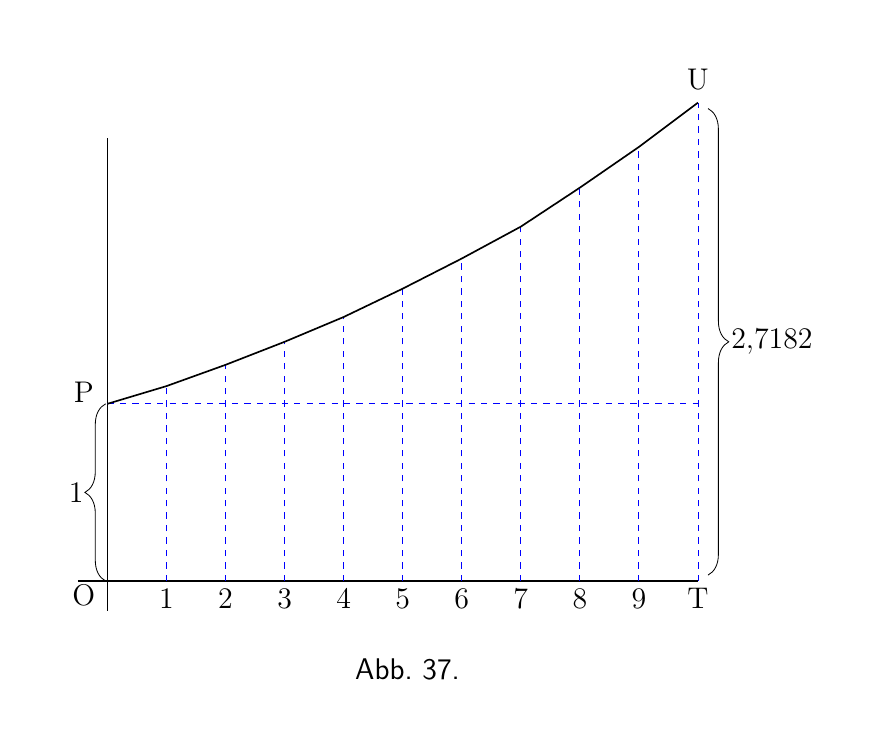
In Abbildung 37 haben wir die entsprechende Darstellung der geometrischen Progression. Jede der aufeinanderfolgenden Ordinaten soll $1 + \dfrac{1}{n}$ sein, also $\dfrac{n+1}{n}$ mal so hoch wie ihr Vorgänger. Die Schritte nach oben sind nicht gleich, denn jeder Schritt nach oben ist nun $\dfrac{1}{n}$ der Ordinate an diesem Teil der Kurve. Hätten wir buchstäblich 10 Schritte, mit $\left(1 + \frac{1}{10} \right)$ für den Multiplikationsfaktor, wäre die Endsumme $(1 + \t frac{1}{10})^{10}$ oder $2,594$ mal das ursprüngliche 1. Nehmen wir aber n hinreichend groß (und das entsprechende $\dfrac{1}{n}$ hinreichend klein), dann ist der Endwert $\left(1 + \dfrac{1}{n}\right)^n$, auf den die Einheit anwächst, $2,71828$.

Epsilon. Dieser geheimnisvollen Zahl $2,7182818$ usw. haben die Mathematiker als Symbol den griechischen Buchstaben $\epsilon$ (ausgesprochen Epsilon) zugeordnet. Alle Schulkinder wissen, dass der griechische Buchstabe $\pi$ (genannt pi) für $3,141592$ usw. steht; aber wie viele von ihnen wissen, dass Epsilon $2,71828$ bedeutet? Dabei ist es eine noch wichtigere Zahl als $\pi$!

Hinweis: Heutzutage wird die Zahl $\epsilon$ als eulersche Zahl (benannt nach dem Mathematiker Leonhard Euler) bezeichnet.

Was also ist Epsilon?

Angenommen, wir würden 1 mit einfachem Zins wachsen lassen, bis es 2 geworden ist; dann, wenn wir 1 mit demselben Nominalzins und für dieselbe Zeit mit echtem Zinseszins wachsen lassen würden, statt mit einfachem, würde es auf den Wert Epsilon wachsen.

Diesen Vorgang, in jedem Augenblick proportional zur Größe in diesem Augenblick zu wachsen, nennen manche Leute eine logarithmische Wachstumsrate. Eine logarithmische Wachstumsrate ist diejenige Rate, die in einer Zeiteinheit 1 auf $2,718281$ anwachsen lässt. Man könnte sie auch als organische Wachstumsrate bezeichnen: Denn es ist charakteristisch für organisches Wachstum (unter bestimmten Umständen), da zu einer bestimmten Zeit der Zuwachs des Organismus proportional zur Größe des Organismus selbst ist. Der umgekehrte Prozess des Zerfallens basiert auch oft auf $\epsilon$.

Wenn wir 100% nehmen als Einheitsrate des Zinssatzes und jede feste Periode als Zeiteinheit, dann ist das Ergebnis, wenn man 1 arithmetisch zur Einheitsrate des Zinssatzes, für eine Zeiteinheit, wachsen lässt, 2, während das Ergebnis, wenn wir 1 logarithmisch mit der Einheitsrate für die gleiche Zeit wachsen lassen, $2,71828\ldots$ ist.

Ein wenig mehr über Epsilon. Wir haben gesehen, dass wir wissen müssen, welchen Wert der Ausdruck $\left(1 + \dfrac{1}{n}\right)^n$ erreicht, wenn n unendlich groß wird. Arithmetisch sind hier eine Menge von Werten tabelliert (die jeder mit Hilfe einer gewöhnlichen Logarithmentabelle ausrechnen kann), die man erhält, wenn man $n = 2$; $n = 5$; $n = 10$; und so weiter, bis $n = 10 000$ annimmt.

\begin{alignat*}{2} &(1 + \tfrac{1}{2})^2 &&= 2,25. \\ &(1 + \tfrac{1}{5})^5 &&= 2,48832. \\ &(1 + \tfrac{1}{10})^{10} &&= 2,59374. \\ &(1 + \tfrac{1}{20})^{20} &&= 2,65329. \\ &(1 + \tfrac{1}{100})^{100} &&= 2,70481. \\ &(1 + \tfrac{1}{1000})^{1000} &&= 2,71692. \\ &(1 + \tfrac{1}{10000})^{10000} &&= 2,71814. \end{alignat*}

Es lohnt sich jedoch, einen anderen Weg zu finden, diese immens wichtige Zahl zu berechnen. Dementsprechend bedienen wir uns des binomischen Theorems und erweitern den Ausdruck $\left(1 + \dfrac{1}{n}\right)^n$ auf diese bekannte Weise.

Der binomische Lehrsatz gibt die Regel, dass:

\begin{align*} (a + b)^n &= a^n + n \dfrac{a^{n-1} b}{1!} + n(n - 1) \dfrac{a^{n-2} b^2}{2!} \\ & \phantom{= a^n\ } + n(n -1)(n - 2) \dfrac{a^{n-3} b^3}{3!} + \text{etc}. \\ \end{align*}

Setzen wir $a = 1$ und $b = \dfrac{1}{n}$, dann erhalten wir:

\begin{align*} \left(1 + \dfrac{1}{n}\right)^n &= 1 + 1 + \dfrac{1}{2!} \left(\dfrac{n - 1}{n}\right) + \dfrac{1}{3!} \dfrac{(n - 1)(n - 2)}{n^2} \\ &\phantom{= 1 + 1\ } + \dfrac{1}{4!} \dfrac{(n - 1)(n - 2)(n - 3)}{n^3} + \text{etc}. \end{align*}

Nun, wenn wir annehmen, dass n unendlich groß wird, sagen wir eine Milliarde oder eine Milliarde Milliarden, dann werden $n - 1$, $n - 2$ und $n - 3$ usw. alle sinnvollerweise gleich n sein; und dann wird die Reihe

\[ \epsilon = 1 + 1 + \dfrac{1}{2!} + \dfrac{1}{3!} + \dfrac{1}{4!} + \text{etc}.\ldots = \sum_{k=0}^{\infty} \dfrac{1}{k!} \]

Indem wir diese schnell konvergierende Reihe zu beliebig vielen Termen nehmen, können wir die Summe bis zu jedem gewünschten Punkt der Genauigkeit ausrechnen. Hier ist die Arbeit für zehn Terme:

	$1.000000$
geteilt durch 1!	$1.000000$
geteilt durch 2!	$0.500000$
geteilt durch 3!	$0.166667$
geteilt durch 4!	$0.041667$
geteilt durch 5!	$0.008333$
geteilt durch 6!	$0.001389$
geteilt durch 7!	$0.000198$
geteilt durch 8!	$0.000025$
geteilt durch 9!	$0.000002$
Summe	$2.718281$

$\epsilon$ ist inkommensurabel mit 1 und ähnelt $\pi$ insofern, als es eine endlose, sich nicht wiederholende Dezimalzahl ist.

Hinweis: Mit n! bezeichnet man das Produkt aller positiven ganzen Zahlen, die kleiner oder gleich n sind. Beispielsweise $3! = 3 \cdot 2 \cdot 1 = 6$. Der Wert von $0!$ ist 1.

Die Exponentialreihe. Wir werden noch eine weitere Reihe brauchen.

Lassen Sie uns, wiederum unter Verwendung des binomischen Satzes, den Ausdruck $\left(1 + \dfrac{1}{n}\right)^{nx}$ erweitern, das ist dasselbe wie $\epsilon^x$, wenn wir n unendlich groß machen.

\begin{align*} \epsilon^x &= 1^{nx} + nx \frac{1^{nx-1} \left(\dfrac{1}{n}\right)}{1!} + nx(nx - 1) \frac{1^{nx - 2} \left(\dfrac{1}{n}\right)^2}{2!} \\ & \phantom{= 1^{nx}\ } + nx(nx - 1)(nx - 2) \frac{1^{nx-3} \left(\dfrac{1}{n}\right)^3}{3!} + \text{etc}.\\ &= 1 + x + \frac{1}{2!} \cdot \frac{n^2x^2 - nx}{n^2} + \frac{1}{3!} \cdot \frac{n^3x^3 - 3n^2x^2 + 2nx}{n^3} + \text{etc}. \\ &= 1 + x + \frac{x^2 -\dfrac{x}{n}}{2!} + \frac{x^3 - \dfrac{3x^2}{n} + \dfrac{2x}{n^2}}{3!} + \text{etc}. \end{align*}

Wenn man aber n unendlich groß macht, vereinfacht sich das zu folgendem:

\[ \epsilon^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + \text{etc.}\dots = \sum_{n=0}^{\infty} \dfrac{x^{n}}{n!} \]

Diese Reihe wird die Exponentialreihe genannt.

Der große Grund, warum $\epsilon$ als wichtig angesehen wird, ist der, dass $\epsilon^x$ eine Eigenschaft besitzt, die keine andere Funktion von x besitzt, dass nämlich bei ihrer Differenzierung ihr Wert unverändert bleibt; oder, mit anderen Worten, ihr Differentialkoeffizient ist derselbe wie sie selbst. Das kann man sofort sehen, wenn man sie nach x differenziert, also:

\begin{align*} \frac{d(\epsilon^x)}{dx} &= 0 + 1 + \frac{2x}{1 \cdot 2} + \frac{3x^2}{1 \cdot 2 \cdot 3} + \frac{4x^3}{1 \cdot 2 \cdot 3 \cdot 4} \\ &\phantom{= 0 + 1 + \frac{2x}{1 \cdot 2} + \frac{3x^2}{1 \cdot 2 \cdot 3}\ } + \frac{5x^4}{1 \cdot 2 \cdot 3 \cdot 4 \cdot 5} + \text{etc}. \\ \text{ or } &= 1 + x + \frac{x^2}{1 \cdot 2} + \frac{x^3}{1 \cdot 2 \cdot 3} + \frac{x^4}{1 \cdot 2 \cdot 3 \cdot 4} + \text{etc}., \end{align*}

das ist genau das gleiche wie die ursprüngliche Reihe.

Nun hätten wir auch den umgekehrten Weg gehen und sagen können: Weiter; lasst uns eine Funktion von x finden, so dass ihr Differentialkoeffizient derselbe ist wie sie selbst. Oder gibt es irgendeinen Ausdruck, der nur Potenzen von x einbezieht, der durch Differenzierung unverändert bleibt? Lassen Sie uns annehmen es gibt einen solchen Ausdruck. Und ihn in der Form des folgenden allgemeinen Ausdrucks schreiben können,

\begin{align*} y &= A + Bx + Cx^2 + Dx^3 + Ex^4 + \text{etc}.,\\ \end{align*}

(wobei die Koeffizienten A, B, $C$ usw. noch bestimmt werden müssen), und differenzieren diesen Ausdruck.

\begin{align*} \dfrac{dy}{dx} &= B + 2Cx + 3Dx^2 + 4Ex^3 + \text{etc}. \end{align*}

Wenn nun dieser neue Ausdruck wirklich derselbe sein soll wie der, aus dem er abgeleitet wurde, ist klar, dass A muss $=B$; dass $C=\dfrac{B}{2}=\dfrac{A}{1 \cdot 2}$; dass $D = \dfrac{C}{3} = \dfrac{A}{1 \cdot 2 \cdot 3}$; dass $E = \dfrac{D}{4} = \dfrac{A}{1 \cdot 2 \cdot 3 \cdot 4}$, usw.

Wenn wir alle Koeffizienten durch einen nur von A abhängigen Ausdruck ersetzen und das A ausklammern erhalten wir den folgenden Ausdruck:

\[ y = A\left(1 + \dfrac{x}{1} + \dfrac{x^2}{1 \cdot 2} + \dfrac{x^3}{1 \cdot 2 \cdot 3} + \dfrac{x^4}{1 \cdot 2 \cdot 3 \cdot 4} + \text{etc}.\right). \]

Wenn wir nun der weiteren Einfachheit halber $A = 1$ nehmen, haben wir

\[ y = 1 + \dfrac{x}{1} + \dfrac{x^2}{1 \cdot 2} + \dfrac{x^3}{1 \cdot 2 \cdot 3} + \dfrac{x^4}{1 \cdot 2 \cdot 3 \cdot 4} + \text{etc}. \]

Wenn man sie beliebig oft differenziert, erhält man immer wieder die gleiche Reihe.

Wenn wir nun den speziellen Fall von $A=1$ nehmen und die Reihe auswerten, erhalten wir einfach

\begin{align*} \text{wenn } x &= 1,\quad & y &= 2,718281 \text{ etc.}; & \text{das ist, } y &= \epsilon; \\ \text{wenn } x &= 2,\quad & y &=(2,718281 \text{ etc.})^2; & \text{das ist, } y &= \epsilon^2; \\ \text{wenn } x &= 3,\quad & y &=(2,718281 \text{ etc.})^3; & \text{das ist, } y &= \epsilon^3; \end{align*}

Und daher

\[ \text{wenn } x=x,\quad y=(2,718281 \text{ etc}.)^x;\quad\text{das ist, } y=\epsilon^x, \]

Und damit ist letztlich gezeigt das

\[ \epsilon^x = 1 + \dfrac{x}{1} + \dfrac{x^2}{1 \cdot 2} + \dfrac{x^3}{1 \cdot 2 \cdot 3} + \dfrac{x^4}{1 \cdot 2 \cdot 3 \cdot 4} + \text{etc}. \]

[Hinweis.-Wie man Exponentialwerte liest . Für diejenigen, die keinen Tutor zur Hand haben, kann es nützlich sein zu sagen, dass $\epsilon^x$ als Epsilon hoch x beziehungsweise als e hoch x gelesen wird; oder manche Leute lesen es als exp x. Also wird $\epsilon^{pt}$ Epsilon hoch der p-t-Potenz oder exp pt gelesen. Nehmen Sie einige ähnliche Ausdrücke: - So wird $\epsilon^{-2}$ e hoch minus zwei oder exp minus zwei gelesen. $\epsilon ^{-ax}$ wird e hoch minus ax oder exp minus ax gelesen.]

Natürlich bleibt $\epsilon^y$ unverändert, wenn nach y differenziert wird. Auch $\epsilon^{ax}$, das gleich $(\epsilon^a)^x$ ist, wird, wenn es nach x differenziert wird, $a\epsilon^{ax}$ sein, weil $a $ eine Konstante ist.

Natürliche oder Napiersche Logarithmen.

Ein weiterer Grund, warum $\epsilon$ wichtig ist, ist, dass es von Napier, dem Erfinder der Logarithmen, zur Grundlage seines Systems gemacht wurde. Wenn y der Wert von $\epsilon^x$ ist, dann ist x der Logarithmus zur Basis $\epsilon$ von y. Oder, wenn

\begin{align*} y &= \epsilon^x, \\ \text{dann}\; x &= \log_\epsilon y. \end{align*}

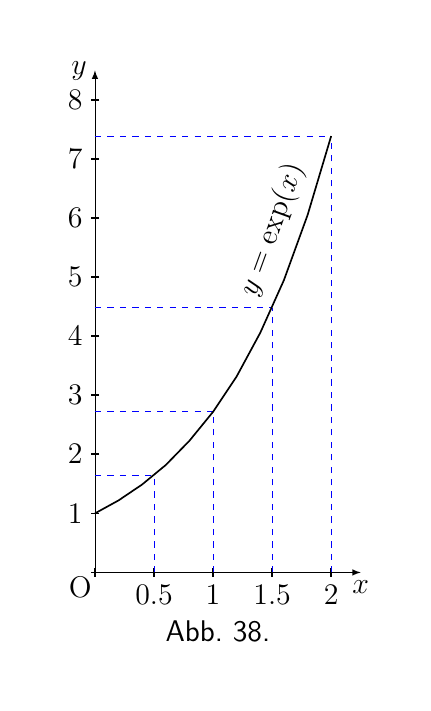
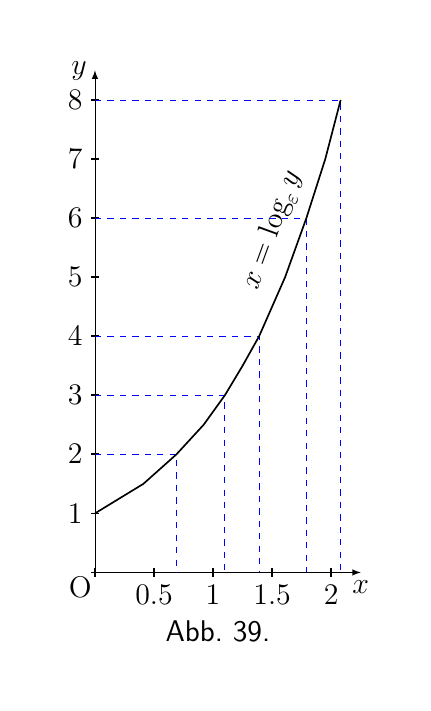
Die beiden Kurven in Abb. 38 und Abb. 39 stellen diese Gleichungen dar.

Die Punkte sind hier berechnet:

Für Abbildung 38:

x	0	$0.5$	1	$1.5$	2
y	1	$1.65$	$2.71$	$4.50$	$7.39$

Für Abbildung 39:

y	1	2	3	4	$8$
x	0	$0.69$	$1.10$	$1.39$	$2.08$

Es ist ersichtlich, dass die Berechnungen zwar unterschiedliche Punkte für die Darstellung ergeben, das Ergebnis jedoch identisch ist. Die beiden Gleichungen bedeuten wirklich dasselbe.

Da viele Personen, die gewöhnliche Logarithmen verwenden, die zur Basis von 10 anstelle von $\epsilon$ berechnet werden, mit den natürlichen Logarithmen nicht vertraut sind, kann es sich lohnen, ein Wort darüber zu verlieren, dass die gewöhnliche Regel, dass das Addieren von Logarithmen den Logarithmus des Produkts ergibt, immer noch gilt;

\[ \log_\epsilon a + \log_\epsilon b = \log_\epsilon ab. \]

Auch die Regel für Potenzen gilt

\[ n \times \log_\epsilon a = \log_\epsilon a^n. \] Aber da 10 nicht mehr die Basis sind, kann man nicht mit 100 oder $1000$ multiplizieren, indem man einfach 2 oder 3 zum Index hinzufügt. Man kann den natürlichen Logarithmus in den gewöhnlichen Logarithmus ändern, indem man ihn einfach mit $0.4343$ multipliziert;

\begin{align*} \log_{10} x &= 0.4343 \times \log_{\epsilon} x, \\ \text{ und umgekehrt,}\; \log_{\epsilon} x &= 2.3026 \times \log_{10} x. \end{align*}

Eine nützliche Tabelle mit napierschen Logarithmen

(Auch natürliche Logarithmen oder hyperbolische Logarithmen genannt)

Nummer	$\log_{\epsilon}$		Nummer	$\log_{\epsilon}$
1	$0,0000$	? ? ? ? ?	$6$	$1,7918$
$1,1$	$0,0953$		7	$1,9459$
$1,2$	$0,1823$		$8$	$2,0794$
$1,5$	$0,4055$		$9$	$2,1972$
$1,7$	$0,5306$		10	$2,3026$
$2,0$	$0,6931$		$20$	$2,9957$
$2,2$	$0,7885$		$50$	$3,9120$
$2,5$	$0,9163$		100	$4,6052$
$2,7$	$0,9933$		2	$5,2983$
$2,8$	$1,0296$		$500$	$6,2146$
$3,0$	$1,0986$		$1000$	$6,9078$
$3,5$	$1,2528$		$2000$	$7,6009$
$4,0$	$1,3863$		$5000$	$8,5172$
$4,5$	$1,5041$		$10 000$	$9,2103$
$5,0$	$1,6094$		$20 000$	$9,9035$

Exponentielle und logarithmische Gleichungen.

Versuchen wir nun, bestimmte Ausdrücke zu differenzieren, die Logarithmen oder Exponenten enthalten.

Nehmen Sie die Gleichung:

\[ y = \log_\epsilon x. \]

Wandeln Sie diese zuerst um in

\[ \epsilon^y = x, \]

da das Differential von $\epsilon^y$ bezüglich y, die ursprüngliche unveränderte Funktion ist (siehe hier),

\[ \frac{dx}{dy} = \epsilon^y, \]

und wenn man von der Umkehrfunktion auf die ursprüngliche Funktion zurückgreift,

\[ \frac{dy}{dx} = \frac{1}{ \dfrac{dx}{dy} } = \frac{1}{\epsilon^y} = \frac{1}{x}. \]

Das ist ein sehr merkwürdiges Ergebnis. Es kann geschrieben werden als

\[ \frac{d(\log_\epsilon x)}{dx} = x^{-1}. \]

Beachten Sie, dass $x^{-1}$ ein Ergebnis ist, das wir nach der Regel für die Differenzierung von Potenzen niemals hätten bekommen können. Diese Regel lautet, mit der Potenz zu multiplizieren und die Potenz um 1 zu reduzieren. Die Differenzierung von x³ ergab also $3x^2$; und die Differenzierung von x² ergab $2x^1$. Aber die Differenzierung von $x^0$ liefert uns nicht $x^{-1}$ oder $0 \times x^{-1}$, weil $x^0$ selbst $= 1$ und eine Konstante ist. Wir werden auf diese merkwürdige Tatsache zurückkommen müssen, dass die Differenzierung von $\log_\epsilon x$ uns $\dfrac{1}{x}$ gibt, wenn wir das Kapitel über die Integration erreichen.

Versuchen Sie jetzt, Folgendes zu differenzieren.

\begin{align*} y &= \log_\epsilon(x+a),\\ \text{das ist }\; \epsilon^y &= x+a; \end{align*}

wir haben $\dfrac{d(x+a)}{dy} = \epsilon^y$, da das Differential von $\epsilon^y$ bleibt $\epsilon^y$.

Dies gibt

\begin{align*} \frac{dx}{dy} &= \epsilon^y = x+a; \\ \end{align*}

daher zurück zur ursprünglichen Funktion, wir erhalten

\begin{align*} \frac{dy}{dx} &= \frac{1}{\;\dfrac{dx}{dy}\;} = \frac{1}{x+a}. \end{align*}

Nächster Versuch

\begin{align*} y &= \log_{10} x. \end{align*}

Ändern Sie zuerst zu natürlichen Logarithmen, indem Sie mit $0,4343$ multiplizieren. Das gibt uns

\begin{align*} y &= 0,4343 \log_\epsilon x; \\ \text{daher }\; \frac{dy}{dx} &= \frac{0,4343}{x}. \end{align*}

Das Nächste ist nicht ganz so einfach. Versuchen Sie dies:

\[ y = a^x. \]

Wenn wir den Logarithmus beider Seiten nehmen (m.a.W. wenn wir beide Seiten logarithmieren), erhalten wir:

\begin{align*} \log_\epsilon y &= x \log_\epsilon a, \\ \text{ bzw. }\; x = \frac{\log_\epsilon y}{\log_\epsilon a} &= \frac{1}{\log_\epsilon a} \times \log_\epsilon y. \end{align*}

Da $\dfrac{1}{\log_\epsilon a}$ eine Konstante ist, erhalten wir:

\[ \frac{dx}{dy} = \frac{1}{\log_\epsilon a} \times \frac{1}{y} = \frac{1}{a^x \times \log_\epsilon a}; \]

Wir kehren zur ursprünglichen Funktion zurück.

\[ \frac{dy}{dx} = \frac{1}{\;\dfrac{dx}{dy}\;} = a^x \times \log_\epsilon a. \]

Wir sehen das:

\[ \frac{dx}{dy} \times \frac{dy}{dx} =1\quad\text{und}\quad \frac{dx}{dy} = \frac{1}{y} \times \frac{1}{\log_\epsilon a},\quad \frac{1}{y} \times \frac{dy}{dx} = \log_\epsilon a. \]

Wir werden feststellen, dass wir immer dann, wenn wir einen Ausdruck wie $\log_\epsilon y =$ eine Funktion von x haben, wir immer mit $\dfrac{1}{y}\, \dfrac{dy}{dx} =$ den Differentialkoeffizienten der Funktion von x haben, so dass wir sofort aus $\log_\epsilon y = x \log_\epsilon a$, hätten schreiben können

\[ \frac{1}{y}\, \frac{dy}{dx} = \log_\epsilon a\quad\text{und}\quad \frac{dy}{dx} = a^x \log_\epsilon a. \]

Versuchen wir nun weitere Beispiele.

Beispiele

(1) $y=\epsilon^{-ax}$. Sei $-ax=z$; dann ist $y=\epsilon^z$. \[ \frac{dy}{dz} = \epsilon^z;\quad \frac{dz}{dx} = -a;\quad\text{also }\quad \frac{dy}{dx} = -a\epsilon^{-ax}. \]

Oder so:

\[ \log_\epsilon y = -ax;\quad \frac{1}{y}\, \frac{dy}{dx} = -a;\quad \frac{dy}{dx} = -ay = -a\epsilon^{-ax}. \]

(2) $y=\epsilon^{\frac{x^2}{3}}$. Sei $\dfrac{x^2}{3}=z$; dann ist $y=\epsilon^z$.

\[ \frac{dy}{dz} = \epsilon^z;\quad \frac{dz}{dx} = \frac{2x}{3};\quad \frac{dy}{dx} = \frac{2x}{3}\, \epsilon^{\frac{x^2}{3}}. \]

Oder so:

\[ \log_\epsilon y = \frac{x^2}{3};\quad \frac{1}{y}\, \frac{dy}{dx} = \frac{2x}{3};\quad \frac{dy}{dx} = \frac{2x}{3}\, \epsilon^{\frac{x^2}{3}}. \]

(3) $y = \epsilon^{\frac{2x}{x+1}}$.

\begin{align*} \log_\epsilon y &= \frac{2x}{x+1},\quad \frac{1}{y}\, \frac{dy}{dx} = \frac{2(x+1)-2x}{(x+1)^2}; \\ \text{ also } \frac{dy}{dx} &= \frac{2}{(x+1)^2} \epsilon^{\frac{2x}{x+1}}. \end{align*}

Prüfen Sie es indem Sie $\dfrac{2x}{x+1}=z$ schreiben.

(4) $y=\epsilon^{\sqrt{x^2+a}}$. $\log_\epsilon y=(x^2+a)^{\frac{1}{2}}$.

\[ \frac{1}{y}\, \frac{dy}{dx} = \frac{x}{(x^2+a)^{\frac{1}{2}}}\quad\text{und}\quad \frac{dy}{dx} = \frac{x \times \epsilon^{\sqrt{x^2+a}}}{(x^2+a)^{\frac{1}{2}}}. \]

Denn wenn $(x^2+a)^{\frac{1}{2}}=u$ und $x^2+a=v$, $u=v^{\frac{1}{2}}$,

\[ \frac{du}{dv} = \frac{1}{{2v}^{\frac{1}{2}}};\quad \frac{dv}{dx} = 2x;\quad \frac{du}{dx} = \frac{x}{(x^2+a)^{\frac{1}{2}}}. \]

Prüfen Sie es indem Sie $\sqrt{x^2+a}=z$ schreiben.

(5) $y=\log(a+x^3)$. Sei $(a+x^3)=z$; dann ist $y=\log_\epsilon z$.

\[ \frac{dy}{dz} = \frac{1}{z};\quad \frac{dz}{dx} = 3x^2;\quad\text{also }\quad \frac{dy}{dx} = \frac{3x^2}{a+x^3}. \]

(6) $y=\log_\epsilon\{{3x^2+\sqrt{a+x^2}}\}$. Sei $3x^2 + \sqrt{a+x^2}=z$; dann ist $y=\log_\epsilon z$.

\begin{align*} \frac{dy}{dz} &= \frac{1}{z};\quad \frac{dz}{dx} = 6x + \frac{x}{\sqrt{x^2+a}}; \\ \frac{dy}{dx} &= \frac{6x + \dfrac{x}{\sqrt{x^2+a}}}{3x^2 + \sqrt{a+x^2}} = \frac{x(1 + 6\sqrt{x^2+a})}{(3x^2 + \sqrt{x^2+a}) \sqrt{x^2+a}}. \end{align*}

(7) $y=(x+3)^2 \sqrt{x-2}$.

\begin{align*} \log_\epsilon y &= 2 \log_\epsilon(x+3)+ \tfrac{1}{2} \log_\epsilon(x-2). \\ \frac{1}{y}\, \frac{dy}{dx} &= \frac{2}{(x+3)} + \frac{1}{2(x-2)}; \\ \frac{dy}{dx} &= (x+3)^2 \sqrt{x-2} \left\{\frac{2}{x+3} + \frac{1}{2(x-2)}\right\}. \end{align*}

(8) $y=(x^2+3)^3(x^3-2)^{\frac{2}{3}}$.

\begin{align*} \log_\epsilon y &= 3 \log_\epsilon(x^2+3) + \tfrac{2}{3} \log_\epsilon(x^3-2); \\ \frac{1}{y}\, \frac{dy}{dx} &= 3 \frac{2x}{(x^2+3)} + \frac{2}{3} \frac{3x^2}{x^3-2} = \frac{6x}{x^2+3} + \frac{2x^2}{x^3-2}. \end{align*}

Denn wenn $y=\log_\epsilon(x^2+3)$, sei $x^2+3=z$ und $u=\log_\epsilon z$.

\[ \frac{du}{dz} = \frac{1}{z};\quad \frac{dz}{dx} = 2x;\quad \frac{du}{dx} = \frac{2x}{x^2+3}. \]

Ähnlich, wenn $v=\log_\epsilon(x^3-2)$, $\dfrac{dv}{dx} = \dfrac{3x^2}{x^3-2}$ und

\[ \frac{dy}{dx} = (x^2+3)^3(x^3-2)^{\frac{2}{3}} \left\{ \frac{6x}{x^2+3} + \frac{2x^2}{x^3-2} \right\}. \]

(9) $y=\dfrac{\sqrt[2]{x^2+a}}{\sqrt[3]{x^3-a}}$.

\begin{align*} \log_\epsilon y &= \frac{1}{2} \log_\epsilon(x^2+a) - \frac{1}{3} \log_\epsilon(x^3-a). \\ \frac{1}{y}\, \frac{dy}{dx} &= \frac{1}{2}\, \frac{2x}{x^2+a} - \frac{1}{3}\, \frac{3x^2}{x^3-a} = \frac{x}{x^2+a} - \frac{x^2}{x^3-a} \\ \text{ und } \frac{dy}{dx} &= \frac{\sqrt[2]{x^2+a}}{\sqrt[3]{x^3-a}} \left\{ \frac{x}{x^2+a} - \frac{x^2}{x^3-a} \right\}. \end{align*}

(10) $y=\dfrac{1}{\log_\epsilon x}$

\[ \frac{dy}{dx} = \frac{\log_\epsilon x \times 0 - 1 \times \dfrac{1}{x}} {\log_\epsilon^2 x} = -\frac{1}{x \log_\epsilon^2x}. \]

(11) $y=\sqrt[3]{\log_\epsilon x} = (\log_\epsilon x)^{\frac{1}{3}}$. Sei $z=\log_\epsilon x$; $y=z^{\frac{1}{3}}$.

\[ \frac{dy}{dz} = \frac{1}{3} z^{-\frac{2}{3}};\quad \frac{dz}{dx} = \frac{1}{x};\quad \frac{dy}{dx} = \frac{1}{3x \sqrt[3]{\log_\epsilon^2 x}}. \]

(12) $y=\left(\dfrac{1}{a^x}\right)^{ax}$.

\begin{align*} \log_\epsilon y &= ax(\log_\epsilon 1 - \log_\epsilon a^x) = -ax \log_\epsilon a^x. \\ \frac{1}{y}\, \frac{dy}{dx} &= -ax \times a^x \log_\epsilon a - a \log_\epsilon a^x. \\ \text{ und } \frac{dy}{dx} &= -\left(\frac{1}{a^x}\right)^{ax} (x \times a^{x+1} \log_\epsilon a + a \log_\epsilon a^x). \end{align*}

Versuchen Sie nun die folgenden Übungen.

Übungen XII

(1) Differenzieren Sie $y=b(\epsilon^{ax} -\epsilon^{-ax})$.

(2) Bestimmen Sie den Differentialkoeffizient bezüglich t für den Ausdruck $u=at^2+2\log_\epsilon t$.

(3) Wenn $y=n^t$ ist, bestimmen Sie $\dfrac{d(\log_\epsilon y)}{dt}$.

(4) Zeigen Sie, dass wenn $y=\dfrac{1}{b} \cdot \dfrac{a^{bx}}{\log_\epsilon a}$ ist, ? ? $\dfrac{dy}{dx}=a^{bx}$ ist.

(5) Wenn $w=pv^n$ ist, bestimmen Sie $\dfrac{dw}{dv}$.

Differenzieren Sie

(6) $y=\log_\epsilon x^n$.

(7) $y=3\epsilon^{-\frac{x}{x-1}}$.

(8) $y=(3x^2+1)\epsilon^{-5x}$.

(9) $y=\log_\epsilon(x^a+a)$.

(10) $y=(3x^2-1)(\sqrt{x}+1)$.

(11) $y=\dfrac{\log_\epsilon(x+3)}{x+3}$.

(12) $y=a^x \times x^a$.

(13) Es wurde von Lord Kelvin gezeigt, dass die Geschwindigkeit der Signalübertragung durch ein Unterseekabel vom Wert des Verhältnisses des Außendurchmessers des Kabels zum Durchmesser des eingeschlossenen Kupferdrahtes abhängt. Nennt man dieses Verhältnis y, so kann die Anzahl der Signale $s$, die pro Minute gesendet werden können, durch die folgende Formel ausgedrückt werden:

\[ s=ay^2 \log_\epsilon \frac{1}{y}; \]

wobei a eine Konstante ist, die von der Länge und der Qualität des Materials abhängt. Zeigen Sie, dass wenn diese gegeben sind, $s$ ein Maximum ist, wenn $y=1 \div \sqrt{\epsilon}$ gilt.

(14) Bestimmen Sie das Maximum oder Minimum von

\[ y=x^3-\log_\epsilon x. \]

(15) Differenzieren Sie $y=\log_\epsilon(ax\epsilon^x)$.

(16) Differenzieren Sie $y=(\log_\epsilon ax)^3$.

Antworten

(1) $ab(\epsilon^{ax} + \epsilon^{-ax})$.

(2) $2at + \dfrac{2}{t}$.

(3) $\log_\epsilon n$.

(5) $npv^{n-1}$.

(6) $\dfrac{n}{x}$.

(7) $\dfrac{3\epsilon^{- \frac{x}{x-1}}}{(x - 1)^2}$.

(8) $6x \epsilon^{-5x} - 5(3x^2 + 1)\epsilon^{-5x}$.

(9) $\dfrac{ax^{a-1}}{x^a + a}$.

(10) $\left(\dfrac{6x}{3x^2-1} + \dfrac{1}{2\left(\sqrt x + x\right)}\right) \left(3x^2-1\right)\left(\sqrt x + 1\right)$.

(11) $\dfrac{1 - \log_\epsilon \left(x + 3\right)}{\left(x + 3\right)^2}$.

(12) $a^x\left(ax^{a-1} + x^a \log_\epsilon a\right)$.

(14) Min.: $y = 0.7$ for $x = 0.694$.

(15) $\dfrac{1 + x}{x}$.

(16) $\dfrac{3}{x} (\log_\epsilon ax)^2$.