Maxima und Minima
Eine der Hauptanwendungen des Differenzierungsprozesses besteht darin, herauszufinden, unter welchen Bedingungen der Wert der differenzierten Funktion (Gleichung) ein Maximum oder ein Minimum wird. Dies ist oft bei technischen Fragen äußerst wichtig, bei denen es am wünschenswertesten ist zu wissen, unter welchen Bedingungen die Arbeitskosten minimal oder die Effizienz maximal wird.
Nun, um mit einem konkreten Fall zu beginnen, nehmen wir die Gleichung
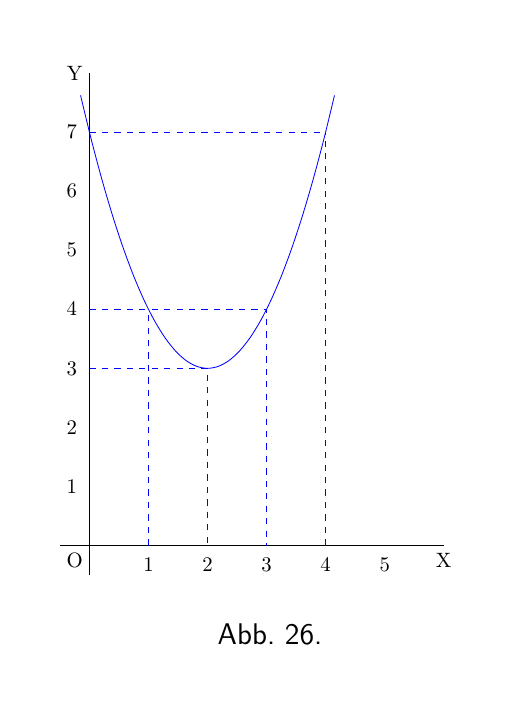
\[ y = x^2 - 4x + 7. \]
Indem wir x eine Reihe von aufeinanderfolgenden Werten zuweisen und die entsprechenden Werte von y finden, können wir leicht erkennen, dass die Gleichung eine Kurve mit einem Minimum darstellt.
| x | $ 0$ | 1 | 2 | 3 | 4 | $ 5$ |
| y | $ 7$ | $ 4 $ | 3 | 4 | 7 | $ 12$ |
Diese Werte sind in Abbildung 26 dargestellt, die zeigt, dass y anscheinend einen Mindestwert von 3 hat, wenn x gleich 2 gesetzt wird. Aber sind Sie sicher, dass das Minimum bei 2 liegt und nicht bei $2 \tfrac{1}{4}$ oder bei $1 \tfrac{3}{4}$?
Natürlich wäre es mit jedem algebraischen Ausdruck möglich, viele Werte zu berechnen und auf diese Weise nach und nach zu einem bestimmten Wert zu gelangen, der ein Maximum oder ein Minimum sein kann.
Hier ist ein anderes Beispiel:
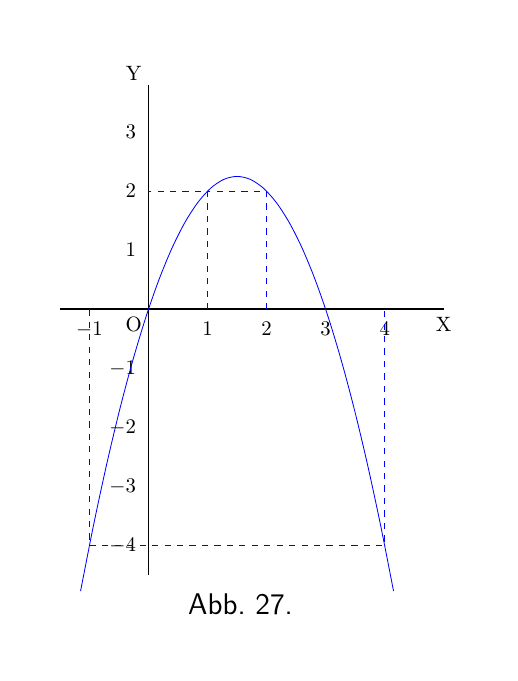
Sei $y = 3x - x^2$.
Berechnen Sie also ein paar Werte:
?
| x | $-1$ | 0 | 1 | 2 | 3 | 4 | 5 |
| y | $-4$ | 0 | 2 | 2 | 0 | $-4$ | $-10$ |
Zeichnen Sie die Werte wie in Abbildung 27.
Es ist offensichtlich, dass es ein Maximum irgendwo zwischen $x = 1$ und $x = 2$ geben wird; und die Kurve sieht so aus, als ob der maximale Wert von y ungefähr $2 \tfrac{1}{4}$ betragen sollte. Probieren Sie einige Werte dazwischen aus. Wenn $ x = 1 \tfrac{1}{4} $, ist $ y = 2.187 $; wenn $x = 1 \tfrac{1}{2}$, $y = 2,25$; wenn $x = 1,6$, $y = 2,24$. Wie können wir sicher sein, dass $2,25$ das wirkliche Maximum ist oder dass es genau dann auftritt, wenn $x = 1 \tfrac{1}{2}$ ist?
Jetzt mag es wie Jonglieren klingen, um sicher zu sein, dass es einen Weg gibt, ohne viele Vorversuche oder Vermutungen direkt zu einem maximalen (oder minimalen) Wert zu gelangen. Und dieser Weg hängt von der Differenzierung ab. Schauen Sie auf eine frühere Seite (hier) zurück, um sich die Bemerkungen zu Abb. 14 und Abb. 15 nochmal anzuschauen und Sie werden sehen, dass immer dann, wenn eine Kurve entweder ihre maximale oder ihre minimale Höhe erreicht, an diesem Punkt $\dfrac{dy}{dx} = 0$ ist. Dies gibt uns nun den Hinweis auf den gesuchten Weg. Wenn Ihnen eine Gleichung vorgelegt wird und Sie den Wert von x finden möchten, der y zu einem Minimum (oder einem Maximum) macht, differenzieren Sie sie zuerst, und nachdem Sie dies getan haben, schreiben Sie $\dfrac{dy}{dx}$ als gleich Null und lösen Sie dann nach x auf. Setzen Sie diesen speziellen Wert von x in die ursprüngliche Gleichung ein, und Sie erhalten dann den erforderlichen Wert von y. Dieser Vorgang wird allgemein als (gleich) Null setzen bezeichnet.
Um zu sehen, wie einfach es funktioniert, nehmen Sie das Beispiel, mit dem dieses Kapitel beginnt, nämlich
\[ y = x^2 - 4x + 7. \]
Differenzieren und wir erhalten
\[ \dfrac{dy}{dx} = 2x - 4. \]
Nun das Ganze gleich null setzen:
\[ 2x - 4 = 0. \]
Diese Gleichung nach x auflösen und wir erhalten:
\begin{align*} 2x &= 4, \\ x &= 2. \end{align*}
Jetzt wissen wir, dass das Maximum (oder Minimum) dann erreicht wird, wenn $x = 2$ ist.
Wir setzen den Wert $x = 2$ in die ursprüngliche Gleichung ein und erhalten dann:
\begin{align*} y &= 2^2 - (4 \times 2) + 7 \\ &= 4 - 8 + 7 \\ &= 3. \end{align*}
Schauen Sie zurück auf Abbildung 26, und Sie werden sehen, dass das Minimum an der Stelle $x = 2$ ist, und dass dieses das Minimum von $y = 3$ ist.
Versuchen Sie ein weiteres Beispiel (Abbildung 24), \begin{align*} y &= 3x - x^2. \\ \text{Differenzieren, }\; \frac{dy}{dx} &= 3 - 2x. \\ \end{align*} gleich null setzen, \begin{align*} 3 - 2x &= 0, \\ \text{daher }\; x &= 1 \tfrac{1}{2}; \\ \end{align*}
Wenn wir diesen Wert für x in die ursprüngliche Gleichung einsetzen erhalten wir:
\begin{align*} y &= 4 \tfrac{1}{2} - (1 \tfrac{1}{2} \times 1 \tfrac{1}{2}), \\ y &= 2 \tfrac{1}{4}. \end{align*}
Dies gibt uns genau die gesuchte Information, und lässt uns nicht wie die Methode des Ausprobierens vieler Werte im Ungewissen.
Nun, bevor wir zu weiteren Fällen übergehen, haben wir zwei Anmerkungen. Wenn Sie aufgefordert werden, $\dfrac{dy}{dx}$ mit null gleichzusetzen, empfinden Sie zunächst (wenn Sie einen eigenen Verstand haben) eine Art Groll, weil Sie wissen, dass $\dfrac{dy} {dx}$ an verschiedenen Stellen der Kurve alle möglichen unterschiedlichen Werte hat, je nachdem, ob sie nach oben oder unten geneigt ist. Wenn Sie also plötzlich aufgefordert werden,
\[ \frac{dy}{dx} = 0, \]
zu schreiben, nehmen Sie es übel und fühlen sich geneigt zu sagen, dass es nicht wahr sein kann. Jetzt müssen Sie den wesentlichen Unterschied zwischen einer Gleichung und einer Bedingungsgleichung verstehen. Normalerweise haben Sie es mit Gleichungen zu tun, die an sich wahr sind, aber bei Gelegenheiten, für die diese Aufgaben Beispiele sind, müssen Sie Gleichungen aufschreiben, die nicht unbedingt wahr sind, sondern nur wahr sind, wenn bestimmte Bedingungen erfüllt sind; und Sie schreiben sie auf, um durch Lösen die Bedingungen zu finden, die sie wahr machen. Nun wollen wir den Wert ermitteln, den x hat, wenn die Kurve weder nach oben noch nach unten geneigt ist, d. h., an der Stelle, an der $\dfrac{dy}{dx} = 0$ ist. Das Schreiben von $\dfrac{dy}{dx} = 0$ bedeutet also nicht, dass es immer $=0$ ist; Sie schreiben es jedoch als Bedingung auf, um zu sehen, welchen Wert x besitzt, wenn $ \dfrac{dy}{dx}$ null ist.
Die zweite Anmerkung ist eine, die Sie (wenn Sie einen eigenen Verstand haben) wahrscheinlich bereits gemacht haben: Nämlich, dass dieser vielbeschworene Prozess der Gleichsetzung mit null Ihnen völlig versagt, ob das x, das Sie dadurch erhalten, zu einem maximalen Wert von y oder einem minimalen Wert von y gehören. Der Prozess unterscheidet nicht selbst; er findet für Sie den richtigen Wert von x, lässt Sie aber selbst herausfinden, ob das entsprechende y ein Maximum oder ein Minimum ist. Wenn Sie die Kurve gezeichnet haben, wissen Sie natürlich bereits, was es sein wird.
Nehmen Sie zum Beispiel die Gleichung:
\[ y = 4x + \frac{1}{x}. \]
Ohne darüber nachzudenken, welcher Kurve sie entspricht, differenziere Sie und setzen Sie diese mit null gleich:
\begin{align*} \frac{dy}{dx} &= 4 - x^{-2} = 4 - \frac{1}{x^2} = 0; \\ \text{ daher }\; x &= \tfrac{1}{2}; \\ \end{align*}
den Wert einsetzen, und
\begin{align*} y &= 4 \end{align*}
wird entweder ein Maximum oder ein Minimum sein. Aber was? In Abhängigkeit von der zweiten Differenzierung wird Ihnen im Folgenden ein Weg aufgezeigt (siehe Kap. XII. ). Aber im Moment reicht es, wenn Sie einfach jeden anderen Wert von x ausprobieren, der ein wenig von dem gefundenen abweicht, und sehen, ob mit diesem geänderten Wert der entsprechende Wert von y kleiner oder größer ist als der bereits gefundene.
Versuchen Sie ein anderes einfaches Problem in Maxima und Minima. Angenommen, Sie sollen eine beliebige Zahl in zwei Teile teilen, sodass das Produkt ein Maximum ist? Wie würden Sie es anstellen, wenn Sie den Trick der Gleichsetzung mit null nicht kennen würden? Ich nehme an, Sie könnten es durch wiederholtes versuchen probieren. Lassen Sie 60 die Zahl sein. Sie können versuchen, die Zahl in zwei Teile zu zerlegen und diese miteinander zu multiplizieren. Somit sind $50$ mal 10 $500$; $52$ mal $8$ ist $416$; $40$ mal $20$ ist $800$; $45$ mal $15$ ist $675$; $ 30 $ mal $ 30 $ ist $ 900 $. Dies sieht nach einem Maximum aus: Versuchen Sie es zu variieren. $31$ mal $29$ ist $899$, was nicht so gut ist; und $32$ mal $28$ ist $896$, was noch schlechter ist. Es scheint also, dass das größte Produkt durch die Aufteilung der Zahl in zwei gleichgroße Hälften erreicht wird.
Sie sehen jetzt, was Ihnen der Calculus sagt. Die in zwei Teile zu zerlegende Zahl sei n. Wenn dann x ein Teil ist, ist der andere $n-x$ und das Produkt ist $x(n-x)$ oder $nx-x^2$. Dann schreiben wir $y=nx-x^2$. Jetzt differenzieren und mit null gleichsetzen;
$\dfrac{dy}{dx} = n - 2x = 0 $
für x lösen, und wir erhalten
$\dfrac{n}{2} = x$
Jetzt wissen wir, dass egal welche Zahl n sein mag, sie in zwei gleiche Teile geteilt werden muss, wenn das Produkt der Teile ein Maximum seien, soll; und der Wert dieses maximalen Produkts ist immer $ = \tfrac{1}{4} n^2$.
Dies ist eine sehr nützliche Regel und gilt für eine beliebige Anzahl von Faktoren, so dass, wenn $m+n+p=$ eine konstante Zahl ist, $m \times n \times p$ ein Maximum ist, wenn $m=n =p$ gilt.
Testfall.
Lassen Sie uns unser Wissen sofort auf einen Fall anwenden, den wir testen können.
\begin{align*} \text{Sei } y &= x^2 - x; \end{align*}
Lassen Sie uns herausfinden, ob diese Funktion ein Maximum oder ein Minimum hat; und wenn ja, testen Sie, ob es ein Maximum oder ein Minimum ist.
Differenzieren und wir erhalten:
\begin{align*} \frac{dy}{dx} &= 2x - 1. \\ \text{ gleich null setzen, wir erhalten }\; 2x - 1 &= 0, \\ \text{dann }\; 2x &= 1, \\ \text{und } \; x &= \tfrac{1}{2}. \end{align*}
Das heißt, wenn x zu $=\frac{1}{2}$ gemacht wird, ist der entsprechende Wert von y entweder ein Maximum oder ein Minimum. Wenn wir also $ x = \frac{1}{2} $ in die ursprüngliche Gleichung einfügen, erhalten wir:
\begin{align*} y &= (\tfrac{1}{2})^2 - \tfrac{1}{2}, \\ \; y &= -\tfrac{1}{4}. \end{align*}
Ist das ein Maximum oder ein Minimum? Um das zu testen, setzen Sie einen Wert für x ein, der ein bisschen größer als $\frac{1}{2}$ ist sagen wir $x=0,6$. Dann erhalten wir:
\[ y = (0,6)^2 - 0,6 = 0,36 - 0,6 = -0,24, \]
Was etwas höher wie $-0,25$ ist; und zeigt, das $y = -0,25$ ein Minimum ist.
Zeichne Sie die Kurve und überprüfen Sie die Berechnung.
Weitere Beispiele.
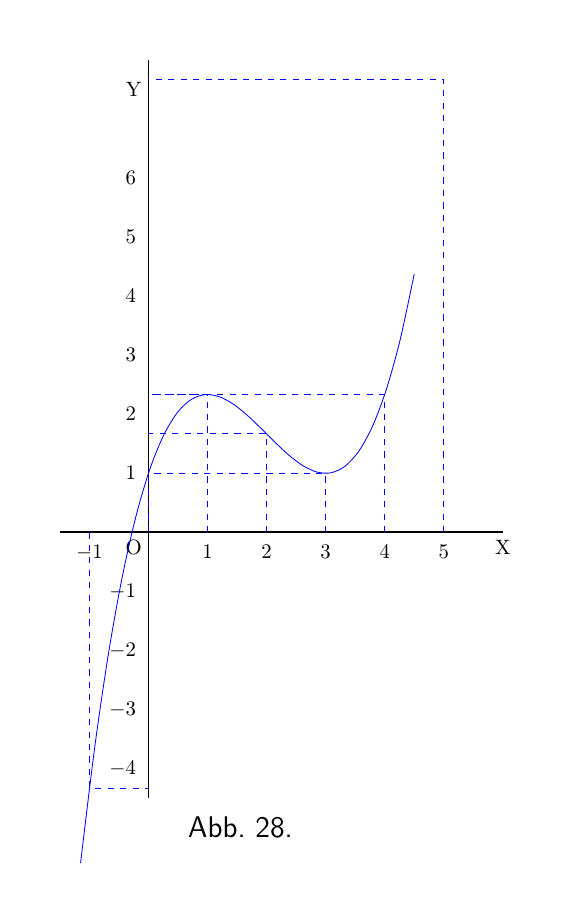
Ein interessantes Beispiel liefert eine Kurve, die sowohl ein Maximum als auch ein Minimum hat. Die Gleichung lautet:
\begin{align*} y &=\tfrac{1}{3} x^3 - 2x^2 + 3x + 1. \\ \text{Dann }\; \dfrac{dy}{dx} &= x^2 - 4x +3. \end{align*}
Gleich null setzen und wir erhalten die quadratische Gleichung:
\[ x^2 - 4x +3 = 0; \]
Und das Lösen der quadratischen Gleichung ergibt zwei Wurzeln, nämlich:
\[ \left\{ \begin{aligned} x &= 3 \\ x &= 1. \end{aligned} \right. \]
Wenn $x=3$ ist, dann ist $y=1$; und wenn $x=1$ ist, dann ist $y=2\frac{1}{3}$. Das erste ist ein Minimum und das zweite ein Maximum.
Die Kurve selbst kann (wie in Abbildung 28) aus den Werten gezeichnet werden, die in der nachfolgenden Tabelle aus der ursprünglichen Gleichung berechnet wurden.
| x | $-1$ | 0 | 1 | 2 | 3 | 4 | 5 | $6$ |
| y | $-4\frac{1}{3}$ | 1 | $2\frac{1}{3}$ | $1\frac{2}{3}$ | 1 | $2\frac{1}{3}$ | $7\frac{2}{3}$ | $19$ |
Eine weitere Übung zu Maxima und Minima bietet das folgende Beispiel:
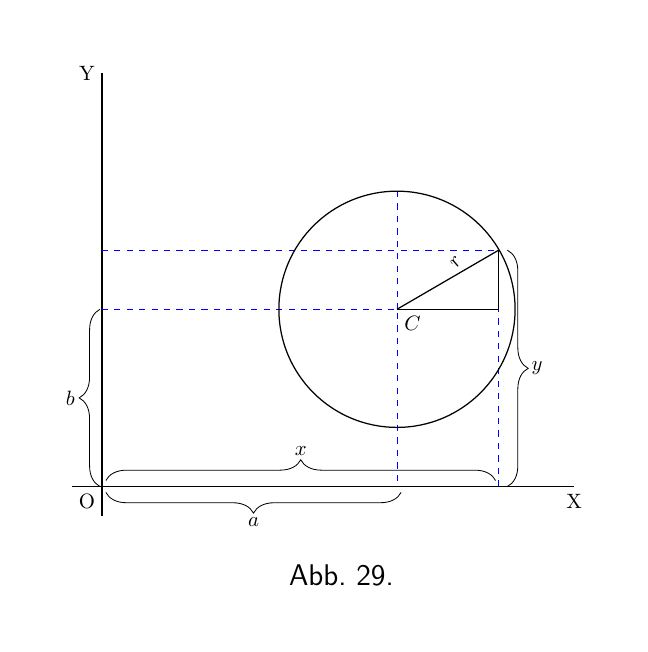
Die Gleichung für einen Kreis mit dem Radius r, dessen Mittelpunkt $C$ an dem Punkt liegt, dessen Koordinaten $x=a$ und $y=b$ sind, wie in Abbildung 29 dargestellt lautet: \[ (y-b)^2 + (x-a)^2 = r^2. \]
Dies kann umgeformt werden zu:
\[ y = \sqrt{r^2-(x-a)^2} + b. \]
Jetzt wissen wir bereits vorher, durch bloße Betrachtung der Figur, dass wenn $ x = a $, y entweder seinen Maximalwert $ b + r $ oder seinen Minimalwert $ b – r $ hat. Aber lassen Sie uns dieses Wissen nicht ausnutzen; Lassen Sie uns herausfinden, welcher Wert von x y zu einem Maximum oder einem Minimum macht, indem wir differenzieren und mit null gleichsetzen.
\begin{align*} \frac{dy}{dx} &= \frac{1}{2} \frac{1}{\sqrt{r^2-(x-a)^2}} \times (2a-2x), \\ \text{das reduziert sich auf }\; \frac{dy}{dx} &= \frac{a-x}{\sqrt{r^2-(x-a)^2}}. \end{align*}
Dann ist die Bedingung dafür, dass y Maximum oder Minimum ist:
\[ \frac{a-x}{\sqrt{r^2-(x-a)^2}} = 0. \]
Da kein Wert von x den Nenner unendlich groß werden lässt, ist die einzige Bedingung, die null ergibt,
\begin{align*} x &= a. \end{align*}
Wenn Sie diesen Wert in die ursprüngliche Gleichung für den Kreis einfügen, finden Sie \begin{align*} y &= \sqrt{r^2}+b; \end{align*}
Und da die Wurzel von $r^2$ entweder $+r$ oder $-r$ ist, haben wir zwei resultierende Werte von y
\begin{align*} \left\{\begin{aligned}y \\ y\end{aligned}\right. & \begin{aligned}= b & + r \\ = b & - r.\end{aligned} \end{align*}
Der Erste davon ist das Maximum oben; der Zweite das Minimum, unten.
Wenn die Kurve so ist, dass es keine Stelle gibt, die ein Maximum oder ein Minimum ist, führt der Vorgang der Gleichsetzung mit null zu einem unmöglichen Ergebnis. Zum Beispiel:
\begin{align*} \text{Sei }\; y &= ax^3 + bx + c. \\ \text{Dann }\; \frac{dy}{dx} &= 3ax^2 + b. \end{align*}
Gleich setzen mit null und wir erhalten $3ax^2 + b = 0$,
\[ x^2 = \frac{-b}{3a}, \quad\text{und}\quad x = \sqrt{\frac{-b}{3a}},\;\text{ was nicht möglich ist.} \]
Daher hat y weder ein Maximum noch ein Minimum.
Ein paar weitere ausgearbeitete Beispiele werden es Ihnen ermöglichen, diese interessanteste und nützlichste Anwendung der Infinitesimalrechnung gründlich zu beherrschen.
(1) Wie lauten die Seiten des Rechtecks mit maximaler Fläche, das in einem Kreis mit Radius $R$ liegt?
Wenn eine Seite x genannt wird, dann ist
\[ \text{die andere Seite} = \sqrt{(\text{Diagonal})^2 - x^2}; \]
Und da die Diagonale des Rechtecks notwendigerweise der Durchmesser ist, ist die andere Seite $ = \sqrt{4R^2 - x^2}$.
Dann ist Fläche des Rechtecks $S = x\sqrt{4R^2 - x^2}$,
\[ \frac{dS}{dx} = x \times \dfrac{d\left(\sqrt{4R^2 - x^2}\,\right)}{dx} + \sqrt{4R^2 - x^2} \times \dfrac{d(x)}{dx}. \]
Wenn Sie vergessen haben, wie man $\sqrt{4R^2-x^2}$ differenziert, hier ein Hinweis: schreiben Sie $4R^2-x^2=w$ und $y=\sqrt{w} $, und bestimmen $\dfrac{dy}{dw}$ und $\dfrac{dw}{dx}$; Probieren Sie es! Und nur wenn Sie es nicht schaffen, schauen Sie noch einmal hier nach.
Sie bekommen \[ \dfrac{dS}{dx} = x \times -\dfrac{x}{\sqrt{4R^2 - x^2}} + \sqrt{4R^2 - x^2} = \dfrac{4R^2 - 2x^2}{\sqrt{4R^2 - x^2}}. \]
Für Maximum oder Minimum müssen wir:
\[ \dfrac{4R^2 - 2x^2}{\sqrt{4R^2 - x^2}} = 0; \] setzen und dass ist, $4R^2 - 2x^2 = 0$ und $x = R\sqrt{2}$.
Die andere Seite ${} = \sqrt{4R^2 - 2R^2} = R\sqrt{2}$; die beiden Seiten sind gleich; die Figur ist daher ein Quadrat. In diesem Fall handelt es sich natürlich um ein Maximum, mit dem wir es zu tun haben.
(2) Welchen Öffnungsradius hat ein konisches Gefäß (Kegel), dessen schräge Seite die Länge l hat, wenn das Fassungsvermögen des Gefäßes am größten ist?
Wenn $R$ der Radius und $H$ die entsprechende Höhe ist, gilt $H = \sqrt{l^2 - R^2}$.
\[ \text{Volumen } V = \pi R^2 \times \dfrac{H}{3} = \pi R^2 \times \dfrac{\sqrt{l^2 - R^2}}{3}. \]
Gehen wir wie in der vorherigen Aufgabe vor, erhalten wir:
\begin{align*} \dfrac{dV}{dR} &= \pi R^2 \times -\dfrac{R}{3\sqrt{l^2 - R^2}} + \dfrac{2\pi R}{3} \sqrt{l^2 - R^2} \\ &= \dfrac{2\pi R(l^2 - R^2) - \pi R^3}{3\sqrt{l^2 - R^2}} = 0 \end{align*}
Für Maximum oder Minimum.
$2\pi R(l^2 - R^2) - \pi R^2 = 0$, und $R = l\sqrt{\tfrac{2}{3}}$, für ein Maximum natürlich.
(3) Bestimmen Sie die Maxima und Minima der Funktion
\[ y = \dfrac{x}{4-x} + \dfrac{4-x}{x}. \]
Wie erhalten:
\[ \dfrac{dy}{dx} = \dfrac{(4-x)-(-x)}{(4-x)^2} + \dfrac{-x - (4-x)}{x^2} = 0 \]
für Maximum oder Minimum; und
\[ \dfrac{4}{(4-x)^2} - \dfrac{4}{x^2} = 0 \quad\text{und}\quad x = 2. \]
Es gibt nur einen Wert, also nur ein Maximum oder Minimum.
\begin{align*} \text{Für}\quad x &= 2,\phantom{.5}\quad y = 2, \\ \text{für}\quad x &= 1,5,\quad y = 2,27, \\ \text{für}\quad x &= 2,5,\quad y = 2,27; \end{align*}
Daher ist es ein Minimum. Es ist aufschlussreich, den Graphen der Funktion zu zeichnen.
(4) Bestimmen Sie die Maxima und Minima der Funktion $y = \sqrt{1+x} + \sqrt{1-x}$. Es wird lehrreich sein, den Graphen zu zeichnen.
Differenzieren ergibt sofort (siehe Beispiel Nr. 1, hier)
\[ \dfrac{dy}{dx} = \dfrac{1}{2\sqrt{1+x}} - \dfrac{1}{2\sqrt{1-x}} = 0 \]
für Maximum oder Minimum.
Da $\sqrt{1+x} = \sqrt{1-x}$ und $x = 0$, die einzige Lösung ist.
Für $x=0$, $y=2$.
Für $x=\pm 0,5$, $y= 1,932$, also ist es ein Maximum.
(5) Bestimmen Sie die Maxima und Minima der Funktion
\[ y = \dfrac{x^2-5}{2x-4}. \]
Wir haben
\[ \dfrac{dy}{dx} = \dfrac{(2x-4) \times 2x - (x^2-5)2}{(2x-4)^2} = 0 \]
für Maximum oder Minimum; und
\[ \dfrac{2x^2 - 8x + 10}{(2x - 4)^2} = 0; \]
$x^2 - 4x + 5 = 0$; wofür
\[ x = \tfrac{5}{2} \pm \sqrt{-1} \]
Lösungen sind.
Da diese imaginär sind, gibt es keinen reellen Wert von x für die $\dfrac{dy}{dx} = 0$ ist; daher gibt es weder ein Maximum noch ein Minimum.
(6) Bestimmen Sie die Maxima und Minima der Funktion
\[ (y-x^2)^2 = x^5. \]
Diese kann, als $y = x^2 \pm x^{\frac{5}{2}}$ geschrieben werden.
\[ \dfrac{dy}{dx} = 2x \pm \tfrac{5}{2} x^{\frac{3}{2}} = 0 \quad\text{für Maximum oder Minimum}; \]
das heißt, $ x (2 \pm \tfrac{5}{2}x^{\ frac{1}{2}}) = 0 $, was für $ x = 0 $ und für $ 2 \pm \tfrac{5}{2} x^{\frac{1}{2}} = 0$ erfüllt ist und auch für $x=\tfrac{16}{25}$. Es gibt also zwei Lösungen.
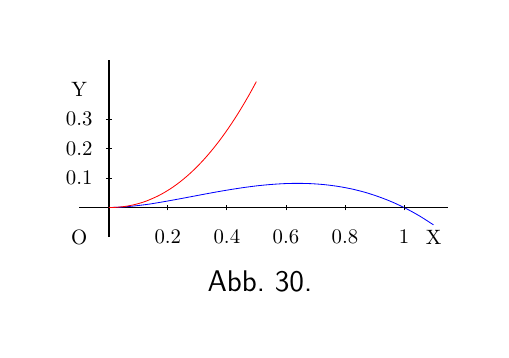
Zuerst nehmen wir $x = 0$. Wenn $x = -0,5$, $y = 0,25 \pm \sqrt[2]{-(0,5)^5}$, und wenn $x = +0,5$, $y = 0,25 \pm \sqrt[2] {(0,5)^5}$. Auf der einen Seite ist y imaginär; das heißt, es gibt keinen Wert von y, der durch einen Graphen dargestellt werden kann; Letztere befindet sich daher vollständig auf der rechten Seite der Achse von y (siehe Abbildung 30).
Beim Zeichnen des Graphen wird festgestellt, dass die Kurve zum Ursprung geht, als ob dort ein Minimum wäre; aber anstatt darüber hinauszugehen, wie es bei einem Minimum der Fall sein sollte, verfolgt es seine Schritte zurück und bildet einen sogenannten "Spitze". Es gibt also kein Minimum, obwohl die Bedingung für ein Minimum erfüllt ist, nämlich $\dfrac{dy }{dx} = 0$. Es ist daher immer notwendig, auf beiden Seiten einen Wert zu nehmen.
Wenn wir nun $x = \tfrac{16}{25} = 0,64$ nehmen. Wenn $x = 0,64$, $y = 0,7373$ und $y = 0,0819$; wenn $x = 0,6$, wird y zu $0,6389$ und zu $0,0811$; und wenn $x = 0.7$ ist, wird y zu $0,8996$ und $0,0804$.
Dies zeigt, dass es zwei Zweige der Kurve gibt; der obere durchläuft kein Maximum, der untere schon.
(7) Ein Zylinder, dessen Höhe doppelt so groß ist wie der Radius der Basis, nimmt an Volumen zu, so dass alle seine Teile immer im gleichen Verhältnis zueinanderstehen; das heißt, der Zylinder ist zu jedem Zeitpunkt dem Originalzylinder ähnlich. Wenn der Radius der Basis r cm beträgt, nimmt die Oberfläche mit einer Geschwindigkeit von $20$ Quadratzentimeter pro Sekunde zu; mit welcher Geschwindigkeit nimmt das Volumen dann zu?
\begin{align*} \text{Fläche } &= S = 2(\pi r^2)+ 2 \pi r \times 2r = 6 \pi r^2.\\ \text{Volumen } &= V = \pi r^2 \times 2r=2 \pi r^3.\\ \frac{dS}{dr} &= 12\pi r,\quad \frac{dV}{dr}=6 \pi r^2,\\ dS &= 12\pi r\, dr=20,\quad dr=\frac{20}{12 \pi r},\\ dV &= 6\pi r^2\, dr = 6 \pi r^2 \times \frac{20}{12 \pi r} = 10r. \end{align*}
Das Volumen ändert sich mit einer Rate von $10r$ Kubiikzentimeter.
Machen Sie sich selbst andere Beispiele. Es gibt nur wenige Themen, die einen solchen Reichtum für interessante Beispiele bieten.
Übung IX
(1) Welche Werte von x machen y zu einem Maximum und einem Minimum, wenn $y=\dfrac{x^2}{x+1}$?
(2)Welcher Wert von x macht y, zu einem Maximum in der Gleichung $y=\dfrac{x}{a^2+x^2}$?
(3) Eine Strecke der Länge $p$ soll in 4-Teile zerlegt und zu einem Rechteck zusammengefügt werden. Zeigen Sie, dass die Fläche des Rechtecks maximal ist, wenn jede seiner Seiten gleich $\frac{1}{4}p$ ist.
(4) Ein Stück Schnur von $30$ cm Länge dessen Enden miteinander verbunden sind, wird durch 3 Stifte gespannt, um ein Dreieck zu bilden. Was ist der größte dreieckige Bereich, der von der Schnur umschlossen werden kann?
(5) Zeichnen Sie die Kurve entsprechend der Gleichung:
\[ y = \frac{10}{x} + \frac{10}{8-x}; \]
Bestimmen Sie $\dfrac{dy}{dx}$, und leiten Sie den Wert von x ab, der y zu einem Minimum macht und bestimmen Sie den Wert von y im Minimum.
(6) Wenn $y = x^5-5x$, finden Sie heraus, welche Werte von x y zu einem Maximum oder einem Minimum machen.
(7) Zeichnen / Fügen Sie ein Quadrat wird in ein bestehendes Quadrat ein. Wann ist das innere Quadrat am größten?
(8) Zeichnen / Fügen Sie einen gegebenen Kegel, dessen Höhe gleich dem Radius der Basis ist, in einen Zylinder
- (a) ein, dessen Volumen maximal ist;
- (b), desen Seitenfläche maximal ist;
- (c), desen Gesamtfläche maximal ist.
(9) Zeichnen / Fügen Sie eine Kugel in einen Zylinder
- (a) ein, dessen Volumen maximal ist;
- (b), desen Seitenfläche maximal ist;
- (c), desen Gesamtfläche maximal ist.
(10) Ein kugelförmiger Ballon nimmt an Volumen zu. Wenn, wenn sein Radius r cm beträgt, und sein Volumen mit einer Geschwindigkeit von 4 Kubikzentimeter pro Sekunde zunimmt, mit welcher Rate nimmt dann seine Oberfläche zu?
(11) Zeichen / Fügen Sie in eine gegebene Kugel einen Kegel ein, dessen Volumen maximal ist.
(12) Der Strom $C$ einer Batterie, die aus $N$ gleichen voltaischen Zellen besteht, ist $C=\dfrac{n \times E}{R+\dfrac{rn^2}{N}}$, wobei E, $R$, r Konstanten sind und n ist die Anzahl der in Reihe geschalteten Zellen. Bestimmen Sie das Verhältnis von n zu $N$, für das der Strom am größten ist.
Antworten
(1) Min.: $x = 0$, $y = 0$; max.: $x = -2$, $y = -4$.
(2) $x = a$.
(4) $25 \sqrt{3}$ Quadratzentimeter.
(5) $\dfrac{dy}{dx} = - \dfrac{10}{x^2} + \dfrac{10}{(8 - x)^2}$; $x = 4$; $y = 5$.
(6) Max. für $x = -1$; min. für $x = 1$.
(7) Verbinden Sie die Mittelpunkte der vier Seiten.
(8) $r = \frac{2}{3} R$, $r = \dfrac{R}{2}$, kein max.
(9) $r = R \sqrt{\dfrac{2}{3}}$, $r = \dfrac{R}{\sqrt{2}}$, $r = 0.8506R$.
(10) Mit einer Rate von $\dfrac{8}{r}$ Quadratzentimeter pro Sekunde.
(11) $r = \dfrac{R \sqrt{8}}{3}$.
(12) $n = \sqrt{\dfrac{NR}{r}}$.