Wie man mit Sinus und Cosinus umgeht
Griechische Buchstaben sind üblich, um Winkel zu bezeichnen, wir nehmen als üblichen Buchstaben für jeden variablen Winkel den Buchstaben $\theta$ (Theta).
Betrachten wir die Funktion:
\[ y= \sin \theta. \]
?
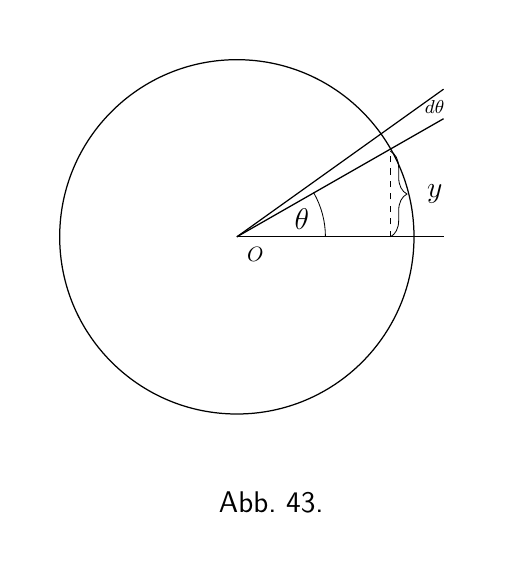
Was wir untersuchen müssen, ist der Wert von $\dfrac{d(\sin\theta)}{d \theta}$; oder anders ausgedrückt, wenn der Winkel $\theta$ variiert, müssen wir die Beziehung zwischen dem Sinusinkrement (der Zunahme von Sinus) und dem Winkelinkrement (der Zunahme des Winkels) finden, wobei beide Inkremente für sich genommen unendlich klein sind. Betrachten Sie Abbildung 43, wobei, wenn der Radius des Kreises eins ist, die Höhe von y der Sinus und $\theta$ der Winkel ist. Wenn nun $\theta$ durch die Addition des kleinen Winkels $d \theta$ - ein Element des Winkels - vergrößert werden soll, wird die Höhe von y, der Sinus, um ein kleines Element dy vergrößert. Die neue Höhe y + dy ist der Sinus des neuen Winkels $\theta + d\theta$ oder, als Gleichung ausgedrückt,
\[ y+dy = \sin(\theta + d \theta); \]
Und wenn die erste Gleichung davon subtrahiert wird, erhalten wir:
\[ dy = \sin(\theta + d \theta)- \sin \theta. \]
Die Größe auf der rechten Seite ist die Differenz zwischen zwei Sinus und Bücher über Trigonometrie zeigen uns, wie man dies berechnet. Denn sie sagen uns, dass, wenn $M$ und $N$ zwei verschiedene Winkel sind,
\[ \sin M - \sin N = 2 \cos\frac{M+N}{2} \cdot \sin\frac{M-N}{2}. \]
Wenn wir dann $M= \theta + d \theta$ für einen Winkel und $N= \theta$ für den anderen setzen, können wir schreiben:
\begin{align*} dy &= 2 \cos\frac{\theta + d\theta + \theta}{2} \cdot \sin\frac{\theta + d\theta - \theta}{2},\\ \text{bzw, }\; dy &= 2\cos(\theta + \tfrac{1}{2}d\theta) \cdot \sin\tfrac{1}{2} d\theta. \end{align*}
Wenn wir aber $d \theta$ als unendlich klein ansehen, dann können wir im Grenzfall $\frac{1}{2} d \theta$ im Vergleich zu $\theta$ vernachlässigen und auch $\sin\frac{1}{2} d \theta$ als dasselbe wie $\frac{1}{2} d \theta$ betrachten. Die Gleichung lautet dann:
\begin{align*} dy &= 2 \cos \theta \times \tfrac{1}{2} d \theta; \\ dy &= \cos \theta \cdot d \theta, \\ \text{ und am Ende, }\; \dfrac{dy}{d \theta} &= \cos \theta. \end{align*}
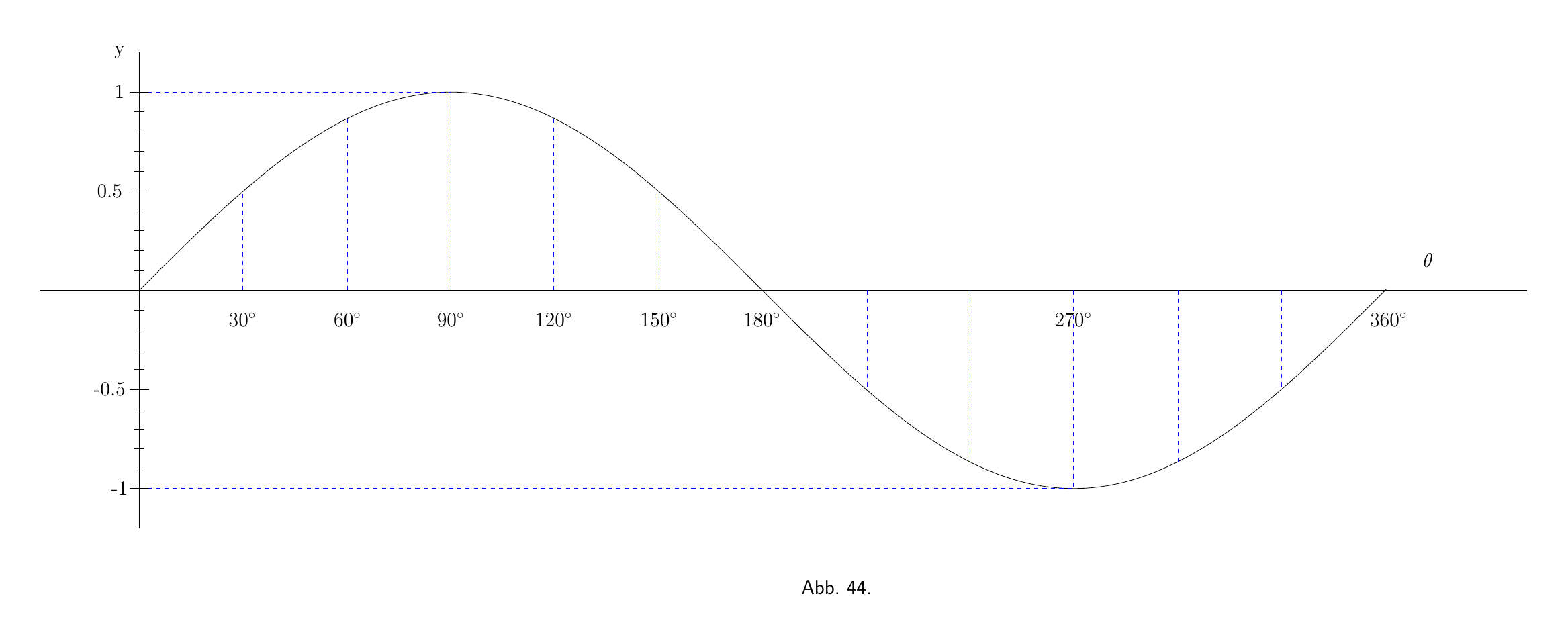
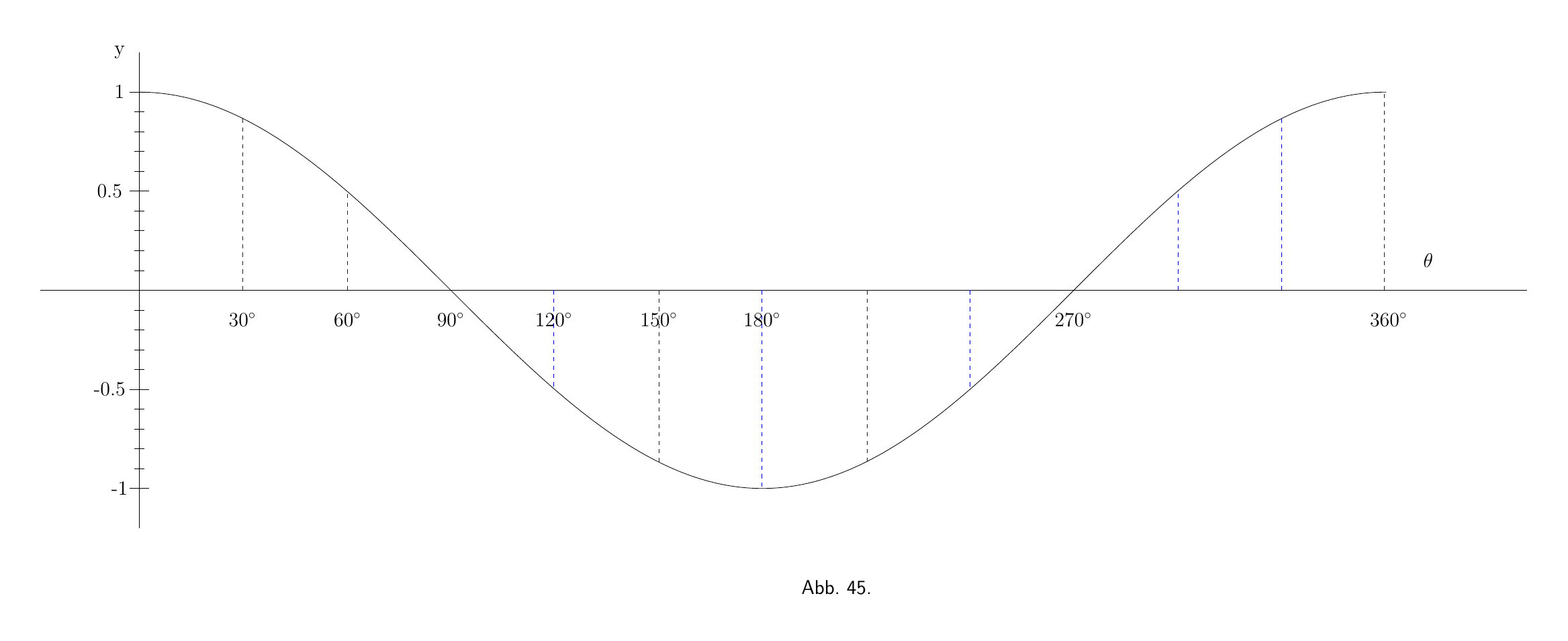
Die beigefügten Kurven, Abb. 44 und Abb. 45 zeigen maßstabsgetreu die Werte von $y=\sin\theta$ und $\dfrac{dy}{d\theta}=\cos\theta$ für die entsprechenden Werte von $\theta $.
Nehmen wir als Nächstes den Cosinus.
Sei $y=\cos \theta$.
Dann $\cos \theta=\sin\left(\dfrac{\pi}{2}-\theta\right)$.
Daher
\begin{align*} &\begin{aligned} dy = d\left(\sin\left(\frac{\pi}{2} - \theta\right)\right) &= \cos\left(\frac{\pi}{2} - \theta\right) \times d(-\theta), \\ &= \cos\left(\frac{\pi}{2} - \theta\right) \times (-d\theta), \end{aligned} \\ &\frac{dy}{d\theta} = -\cos\left(\frac{\pi}{2} - \theta\right). \end{align*}
Und es folgt, dass:
\begin{align*} &\frac{dy}{d\theta} = -\sin \theta. \end{align*}
Schließlich nehmen Sie die Tangente. Sei
\begin{align*} y &= \tan \theta, \\ dy &= \tan(\theta + d\theta) - \tan\theta. \\ \end{align*}
Erweitern Sie, wie in Büchern über Trigonometrie gezeigt wird,
\begin{align*} \tan(\theta + d\theta) &= \frac{\tan\theta + \tan d\theta} {1 - \tan\theta \cdot \tan d\theta}; \\ \text{dann }\; dy &= \frac{\tan\theta + \tan d\theta} {1-\tan\theta \cdot \tan d\theta} - \tan\theta \\ &= \frac{(1 + \tan^2\theta)\tan d\theta} {1-\tan\theta \cdot \tan d\theta}. \end{align*}
Denken Sie daran, dass, wenn $d\theta$ unendlich verkleinert wird, der Wert von $\tan d\theta$ mit $d\theta$ identisch wird und $\tan\theta \cdot d\theta$ vernachlässigbar klein ist verglichen mit 1, so dass sich der Ausdruck auf:
\begin{align*} dy &= \frac{(1+\tan^2 \theta)\, d\theta}{1}, \\ \text{so that }\; \frac{dy}{d\theta} &= 1 + \tan^2\theta, \\ \text{or}\; \frac{dy}{d\theta} &= \sec^2 \theta \end{align*}
reduziert.
Sammeln wir diese Ergebnisse, und wir erhalten:
| y | $\dfrac{dy}{d\theta}$ |
|---|---|
| $\sin\theta$ | $\cos\theta$ |
| $\cos\theta$ | $-\sin\theta$ |
| $\tan\theta$ | $\sec^2\theta$ |
Manchmal haben wir es in mechanischen und physikalischen Fragen, wie zum Beispiel bei einfachen harmonischen Bewegungen und bei Wellenbewegungen, mit zunehmenden Winkeln, im Verhältnis zur Zeit, zu tun. Wenn also T die Zeit einer vollständigen Periode oder einer Bewegung um den Kreis ist, dann ist der Winkel rund um den Kreis $2\pi$ Radiant oder $360^{\circ} $, der Betrag des in der Zeit t bewegten Winkels, wird:
\begin{align*} \theta &= 2\pi\frac{t}{T},\quad \text{in Radian,} \\ \text{or }\; \theta &= 360\frac{t}{T},\quad \text{in Grad.} \end{align*}
Wenn die Frequenz oder die Anzahl / Häufigkeiten der Perioden pro Sekunde mit n bezeichnet wird, dann ist $n = \dfrac{1}{T}$, und wir können dann schreiben:
\[ \theta=2\pi nt. \]
Dann haben wir:
\[ y = \sin 2\pi nt. \]
Wenn wir nun wissen wollen, wie sich der Sinus zeitlich ändert, müssen wir nicht nach $\theta$, sondern nach t differenzieren. Dazu müssen wir auf den in Kapitel IX erklärten Kunstgriff zurückgreifen und setzen:
\[ \frac{dy}{dt} = \frac{dy}{d\theta} \cdot \frac{d\theta}{dt}. \]
Jetzt ist $\dfrac{d\theta}{dt}$ offensichtlich $2\pi n$; und damit:
\begin{align*} \frac{dy}{dt} &= \cos \theta \times 2\pi n \\ &= 2\pi n \cdot \cos 2\pi nt. \\ \end{align*}
In ähnlicher Weise folgt daraus
\begin{align*} \frac{d(\cos 2\pi nt)}{dt} &= -2\pi n \cdot \sin 2\pi nt. \end{align*}